"Großer Satz" von Feuerbach

Der Feuerbachkreis eines Dreiecks ABC berührt stets den Inkreis und die drei Ankreise und zwar den Inkreis innerlich und die drei Ankreise äußerlich.

Karl Wilhelm Feuerbach war weder der Erstentdecker des Feuerbachkreises noch wusste er, dass die Eulerpunkte Ea, Eb und Ec auf jenem liegen. Dieser Satz ist der Grund, warum der Kreis trotzdem seinen Namen erhielt.
(in der englischen Literatur wird meist vom "nine-point circle", also vom Neunpunktekreis gesprochen)



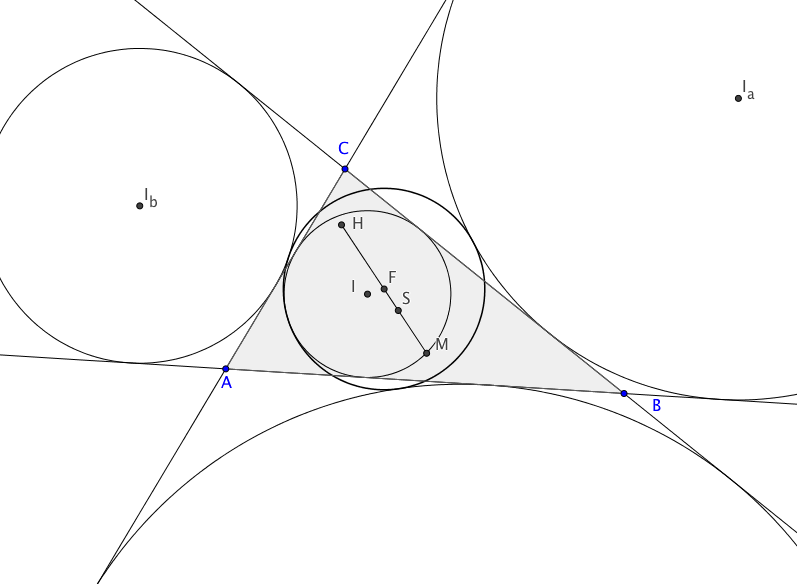
Dieser Satz definiert ein weiteres Dreieckszentrum. Der Berührpunkt des Feuerbach-Kreises mit dem Inkreis wird als Feuerbachpunkt bezeichnet und nicht, wie man vermuten könnte, der Mittelpunkt F des Feuerbach-Kreises. In der Kimberling-Liste wird der Feuerbachpunkt als X11 aufgeführt.
In der Abbildung sind H der Höhenschnittpunkt, S der Schwerpunkt und M der Umkreismittelpunkt des Dreiecks ABC. Die Strecke markiert somit die Eulergerade, auf der der Mittelpunkt F des Feuerbachkreises ebenfalls liegt.

Beweis:

Um diesen Satz zu beweisen, wird die Inversion am Kreis und folgende Konstruktion benutzt: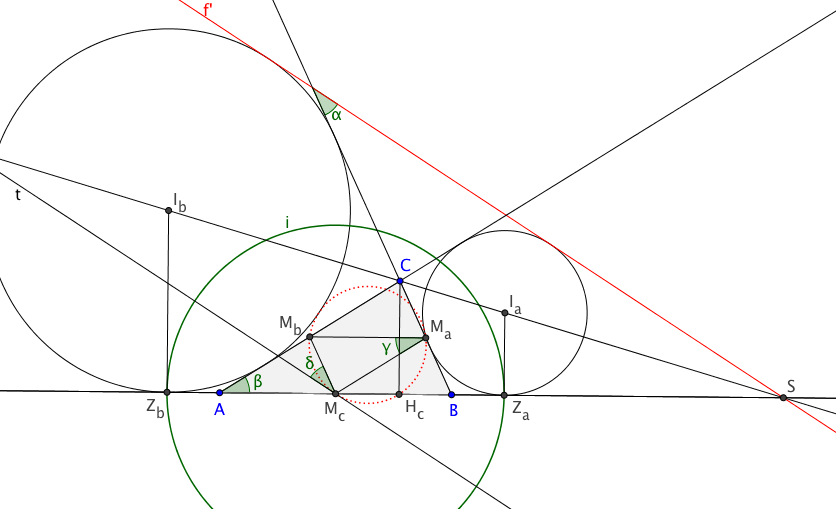

 

Beweisidee: Man konstruiert einen Inversionskreis i, der die beiden Ankreise rechtwinkelig schneidet (damit sie auf sich selbst abgebildet werden). Man kann dann zeigen, dass der Feuerbachkreis durch die Inversion an i auf die gemeinsame Tangente f' der beiden Ankreise abgebildet wird. Da die Tangente die Ankreise berührt, berührt der Feuerbachkreis ebenfalls die Ankreise.

Man betrachte die Ankreise der Dreiecksseiten a und b. Ihre Mittelpunkte seien Ia und Ib, ihre Berührpunkte mit der Geraden durch A und B seien Za und Zb. Weiterhin seien Ma, Mb und Mc die Mittelpunkte der Seiten des Dreiecks ABC.
Dann gilt (siehe hier) für die Entfernung zwischen einem Eckpunkt und dem gegenüberliegenden Ankreisberührpunkt: , so dass Mc auch der Mittelpunkt von ZaZb ist. Der Kreis i um Mc mit dem Radius |McZb| verläuft also auch durch Za.
Die Punkte C und S teilen die Strecke IaIb innerlich und äußerlich im gleichen Teilungsverhältnis, nämlich dem der Radien der Ankreise. Die vier Punkte Ib, Ia, C und S sind also harmonische Punkte.
Projiziert man diese vier Punkte Ib, Ia, C und S senkrecht auf die Gerade AB, so erhält man die vier Punkte Zb, Za, Hc und S, die folglich auch harmonische Punkte sind.

Wir betrachten nun die Inversion am Kreis i und bestimmen zu einigen Objekten die Bildpunkte.
Der Höhenfußpunkt Hc wird auf den Punkt S abgebildet, da Zb, Za, Hc und S harmonische Punkte sind. (Begründung am Ende der Information über harmonische Punkte )
Die Ankreise an die Dreiecksseite a und b werden auf sich selbst abgebildet, da sie den Inversionskreis i senkrecht schneiden. Das erkennt man am deutlichsten in den Schnittpunkten Za und Zb. Die Begründung der Abbildungseigenschaft findet man hier.
Der Feuerbachkreis (rot gepunktet) des Dreiecks ABC wird auf die Gerade f' abgebildet, die zweite äußere, gemeinsame Tangente der beiden Ankreise.

Begründung
Der Feuerbachkreis verläuft durch den Mittelpunkt Mc des Inversionskreises. Also ist das Bild des Feuerbachkreises eine Gerade, die
1. durch den Bildpunkt eines Punktes der Kreislinie verläuft und
2. parallel zur Tangente an den Feuerbachkreis im Punkt Mc ist.
(Die zugehörigen Eigenschaften der Inversion am Kreis findet man hier)

Die 1. Bedingung wird vom Punkt Hc erfüllt, der bei der Inversion an i auf S abgebildet wird.
Nun betrachte man die Tangente t an dem Feuerbachkreis im Punkt Mc. Der von t und der Strecke MbMc eingeschlossenen Winkel ist δ. Die 2. Eigenschaft ist erfüllt, wenn wir zeigen, dass t und f' parallel sind. Da MbMc parallel zu BC ist, zeigen wir dazu, dass der Winkel δ so groß ist wie der Winkel α, der Winkel zwischen f' und der Geraden BC.

Es gilt:

γ=δ      δ ist Sehnen-Tangenten-Winkel, γ ist Peripheriewinkel zur Sehne MbMc und dem Feuerbachkreis (Hintergrund ist der Peripheriewinkelsatz)
β=γ      MaMb ist parallel zu AB und MaMc ist parallel zu AC
α=β      Bei der Spiegelung an der Geraden IaIb wird die Gerade AB auf f' und die Gerade AC auf die Gerade BC abgebildet. Damit ist α der Bildwinkel von β und damit sind beide Winkel gleich groß.

Folglich ist t parallel zu f' und wir haben gezeigt, dass das Inversionsbild des Feuerbach-Kreises die Gerade f' ist.

Da die Inversion am Kreis involutorisch (selbstinvers) ist und die Inversion die Berühreigenschaften erhält (das ist eine Folgerung aus der Winkeltreue), gilt:
f' berührt als gemeinsame Tangente die beiden Ankreise. Also berührt das Urbild von f', der Feuerbachkreis, auch die Urbilder der beiden Ankreise, die aber auf sich selbst zurückabgebildet werden.

Bleibt noch zu zeigen, dass auch der Inkreis und der Ankreis an die Seite AB den Feuerbach-Kreis berühren.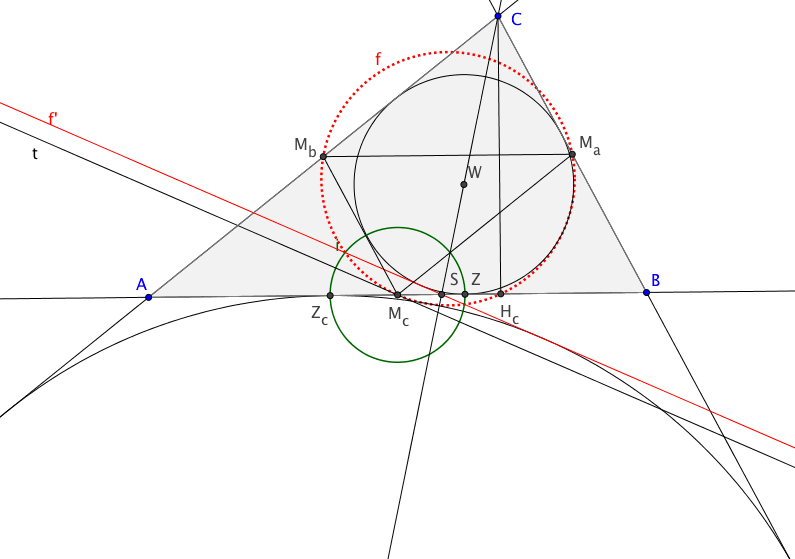
Dazu betrachte man folgende Konstruktion:

Zc ist der Berührpunkt des Ankreises an die Seite AB, Z der Berührpunkt des Inkreises mit dieser Seite. Wie oben seien Ma, Mb und Mc die Mittelpunkte der Seiten des Dreiecks ABC.
Dann kann man mit demselben Hinweis (siehe hier) zeigen, dass Zc und Z wieder symmetrisch zu Mc liegen. Folglich geht der Kreis mit dem Mittelpunkt Mc und dem Radius |McZc| auch durch Z und bildet für die weiteren Betrachtungen den Inversionskreis i.
S sei der Schnittpunkt der Winkelhalbierenden des Winkels ACB mit der Seite AB. Die vier Punkte C, W, S und Ic (der Mittelpunkt des Ankreises) liegen auf dieser Winkelhalbierenden und sind harmonische Punkte. Projiziert man diese vier Punkte senkrecht auf die Gerade AB, so erhält man Hc, Z, S und Zc. Damit ist gezeigt, dass bei der Inversion an i Hc auf S abgebildet wird.
Es sei nun f' die eine gemeinsame, innere Tangente an den Inkreis und den Ankreis. Analog zur Argumentation oben lässt sich zeigen, dass f' das Bild des Feuerbach-Kreises bei Inversion an i ist. Damit ist letztlich gezeigt, dass der Feuerbachkreis den Inkreis (und den Ankreis an die Seite AB) berührt.
zurück

Matthias Pahl, R.Albers, Erstellt mit GeoGebra