Harmonische Teilung

Die harmonische Teilung bezeichnet ein besonderes Lageverhältnis von vier Punkten auf einer Geraden.
Eine harmonische Teilung liegt vor, wenn eine Strecke AB durch zwei weitere Punkte T und U innen und außen so geteilt wird, dass die beiden Teilverhältnisse und den gleichen Betrag haben. Wird also die Strecke AB von Punkt T innerlich im Verhältnis geteilt, so existiert ein Punkt U, der die Strecke AB äußerlich in demselben Verhältnis teilt. Es gilt dann:
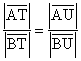(1)
T und U sind somit harmonische Teilpunkte zu AB.

Satz: Teilen T und U die Strecke AB harmonisch, so teilen auch A und B die Strecke TU harmonisch.

Beweis: Durch Umstellen von Gleichung (1) folgt, dass 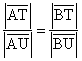gilt. Es liegt also wieder eine harmonische Teilung vor.
Nach untenstehender Konstruktion wird die Strecke AB von T im Verhältnis geteilt.
Sei o.B.d.A. die Steckenlänge AB=1, dann gilt für die Strecken AT, BT, AU und BU:

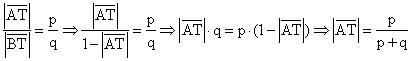
Analog ergibt sich:
Für BU gilt:

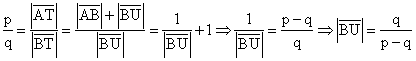
Für AU gilt:

Einsetzen in liefert:

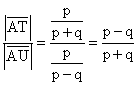
Daraus folgt: Teilen die Punkte T und U die Strecke AB harmonisch im Verhältnis p:q, dann wird die Strecke TU von A und B im Verhältnis (p-q):(p+q) harmonisch geteilt. Man nennt deshalb die Punkte A, B, T und U vier harmonische Punkte.

Konstruktion

Die Punkte A, B und T sind gegeben und liegen auf einer Geraden. Der Punkt U soll so konstruiert werden, dass A,B,T und U vier harmonische Punkte sind.

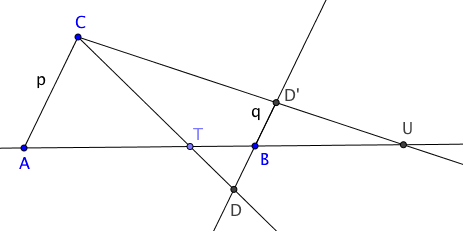
Der Punkt C wird beliebig gewählt, die Geraden AC und BD sind parallel. Punkt D ergibt sich durch die Verbindung von C mit dem gegebenen Teilpunkt T. D wird nach D' übertragen, die Strecken BD und BD' sind gleich lang. Der fehlende Teilpunkt ergibt sich durch die Verbindung von C mit D'.

Da die die Geraden AC und BD parallel sind, gilt nach dem zweiten Strahlensatz mit Zentrum U:

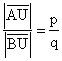
Da BD=BD'=q gilt nach dem zweiten Strahlensatz mit Zentrum T:

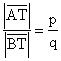
Die Strecke AB wird also von den Punkten T und U innerlich und äußerlich im Verhältnis geteilt. Damit sind A, B, T und U vier harmonische Punkte.

Harmonisch Teilung und die Inversion am Kreis

Der Punkt P' ist der Bildpunkt von P bezüglich der Spiegelung am Kreis k.
A und B sind die Endpunkte auf dem Durchmesser des Kreises k, Strecke AB wird durch P und P' harmonisch geteilt. Die Punkte A, B, P,P' sind also vier harmonische Punkte

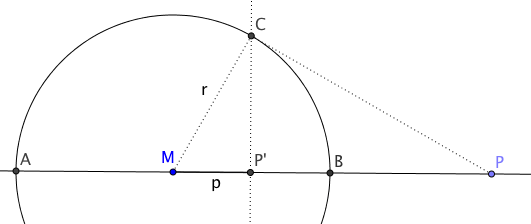
Sei die Strecke MP'=p und r der Radius von k, dann gilt:

|AP'| = p+r

|MP| = r²/p nach Kathetensatz in Dreieck MPC

|AP| = r+r²/p

|BP'| = r-p

|BP| = r²/p - r

Nun ist zu zeigen:

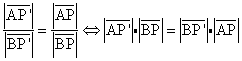
Einsetzen liefert:

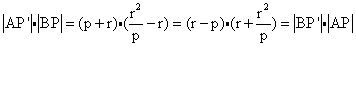
Die Punkte A, B, P, P' bilden also vier harmonische Punkte.

zurück

Matthias Pahl, Erstellt mit GeoGebra