Definition

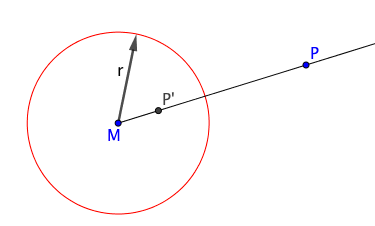
Man betrachte einen Kreis mit dem Mittelpunkt M und dem Radius r. Die Inversion an diesem Kreis ist für jeden Punkt P der Zeichenebene außer dem Mittelpunkt M nach folgender Vorschrift definiert:

• Der Bildpunkt P' liegt auf der Halbgeraden MP.


• Für die Abstände zwischen dem Bildpunkt P' bzw dem Punkt P und M gilt: |P'M| |PM |= r².

Konstruktion des Bildpunktes

Bei der Konstruktion von P' werden zwei Fälle unterschieden:

1. P liegt innerhalb des Inversionskreises.
2. P liegt außerhalb des Kreises.

• Das Kreisinnere wird eindeutig auf das Kreisäußere abgebildet und umgekehrt.
• Die Punkte auf der Kreislinie sind Fixpunkte.
• Die Abbildung ist eine Involtion: Wendet man sie auf einen Punkt P und dann nochmals auf P' an, so erhält man wieder den Ursprünglichen Punkt (P''=P).
• Nähert sich P dem Mittelpunkt M, so entfernt sich P' unbeschränkt weit vom Kreis. Wandert umgekehrt P immer weiter weg vom Kreis, nähert sich P' dem Mittelpunkt M. Der Bildpunkt von M ist ein unendlich ferner Punkt.
• Sind A und B die Endpunkte auf dem Durchmesser des Kreises k, wird die Strecke AB durch P und P' harmonisch geteilt.
• Abbildung von Geraden:
  • Geraden, die durch den Mittelpunkt des Inversionskreises gehen, werden auf sich selbst abgebildet.
  • Geraden, die nicht durch den Mittelpunkt gehen, werden auf Kreise abgebildet, die durch den Mittelpunkt gehen.
  Experimentierdatei
• Abbildung von Kreisen:
  • Kreise, die durch M verlaufen, werden auf Geraden abgebildet, die nicht durch den Mittelpunkt verlaufen.
  • Kreise, die nicht durch M gehen, werden wieder auf solche abgebildet.
  • Kreise, die den Inversionskreis rechtwinkelig schneiden, werden auf sich selbst abgebildet.
  Experimentierdatei
• Die Abbildung ist winkeltreu Konstruktion
• Berühreigenschaften bleiben erhalten.

zurück zum Beweis

Matthias Pahl, erstellt mit GeoGebra