Winkeltreue der Inversion am Kreis

Durch Spiegeln am Kreis werden Geraden zu Kreisen (durch den Mittelpunkt des Inversionskreises) und umgekehrt. Hier ist der rote Kreis a' Abbild der roten Gerade a und der grüne Kreis b' Abbild der grünen Gerade b. Offensichtlich ist der Winkel α im Punkt P zwischen den Geraden genauso groß wie der Winkel β im Punkt P' zwischen den Kreistangenten, welcher dem Schnittwinkel der beiden Kreise entspricht.

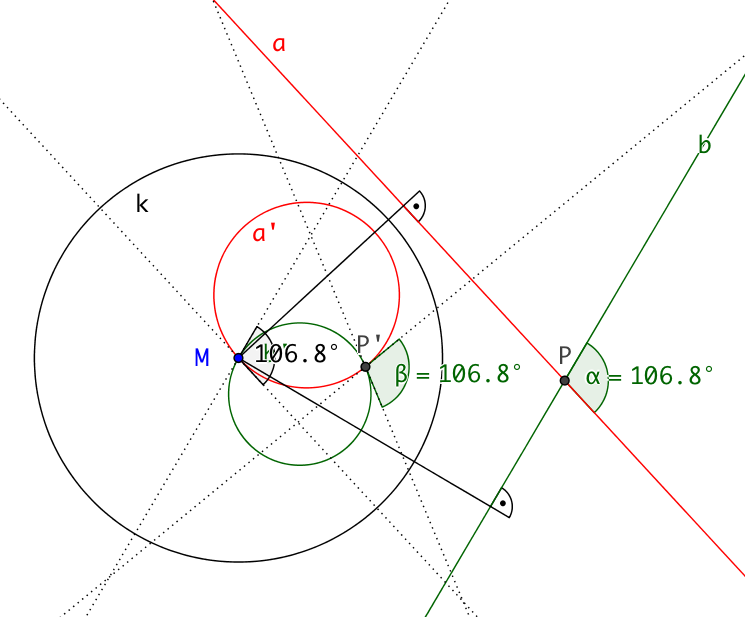
Nach Link ist die Tangente am Bild der Geraden im Inversionszentrum M parallel zur dieser Geraden. Somit müssen sich die Kreise in M unter demselben Winkel schneiden wie die Geraden. Da die Schnittwinkel von zwei Kreisen immer gleich sind, schneiden sich die Kreise in beiden Schnittpunkten unter diesem Winkel.

Matthias Pahl, Erstellt mit GeoGebra