Der Kreis c geht durch den Mittelpunkt M des Inversionskreises i.

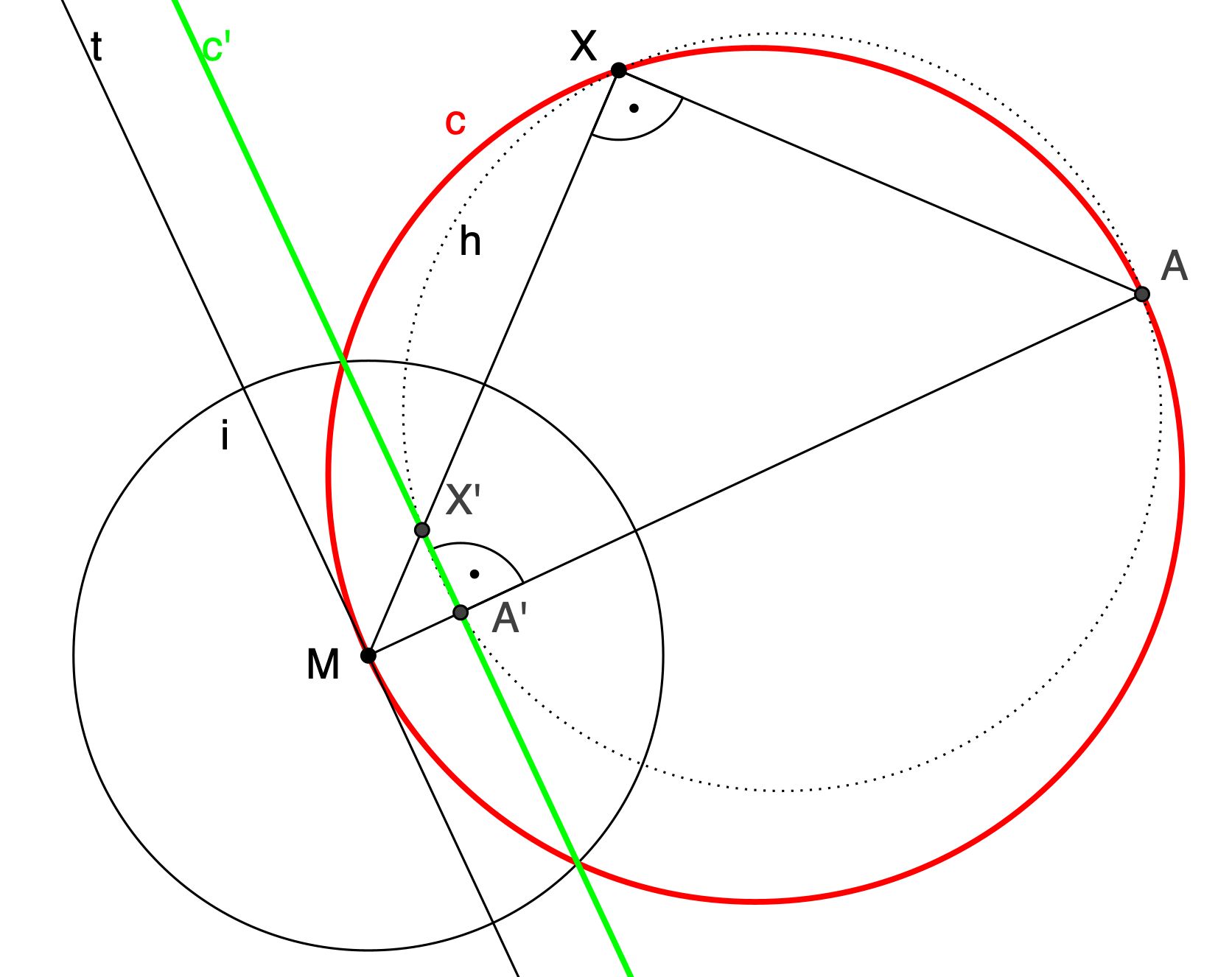
Sei MA der Durchmesser von c durch den Punkt M und sei A' der inverse Punkt zu A. r ist der Radius des Inversionskreies i.
Dann gilt: .
Sei X ein beliebiger Punkt auf c und X' ist sein Inverses. Dann gilt ebenfalls: .
Somit liegen A, X, X', A' auf einem Kreis h (Umkehrung des Sekantensatzes).

Da der Winkel (Satz des Thales am Kreis c über dem Durchmesser MA) ist X'A Durchmesser des Kreises h. Dann gilt (Satz des Thales am Kreis h).
Läuft nun X auf dem Kreis c, so bleibt MA unverändert. X' verläuft also auf einer zur Strecke MA senkrechten Geraden c' durch A'.
Diese Gerade c' ist parallel zur Tangente t an c im Punkt M.

Folgerung:

Gegeben ist ein Inversionskreis i mit dem Mittelpunkt M, ein Kreis c, der durch M verläuft, ein Punkt X auf c und ein Punkt X', der Bildpunkt zu X ist bei Inversion an i. Eine Gerade g, die durch X' verläuft und parallel zu t ist, ist dann das Bild c' von c bei Inversion an i.

Matthias Pahl, Reimund Albers, Erstellt mit GeoGebra