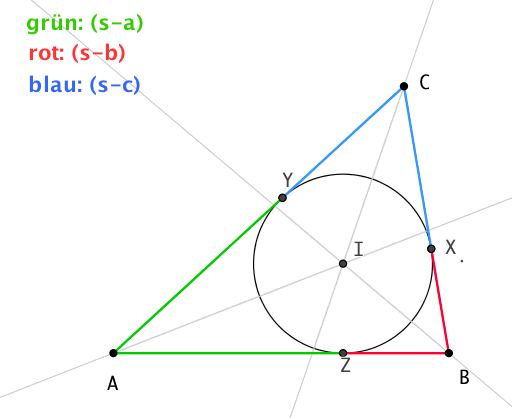
Durch die Berührpunkte des Inkreises werden die Seiten des Dreiecks in zwei Teile geteilt. Mit s als dem halben Umfang können diese Teile prägnant angegeben werden.

Herleitung

Seien die Berührpunkte X, Y und Z. Dann gilt für den Umfang des Dreiecks:

U = 2s = a+b+c = |AZ| + |ZB| + |BX| + |XC| + |CY| + |YA|

Da die Abschnitte auf den beiden Tangenten von einem Punkt gleich lang sind (Symmetrie), gilt:

|AZ| = |YA| , |ZB| = |BX| , |XC| = |CY| oder

Dann ist |AZ| = s - |BX| - |CY| = s - (|BX| + |XC|) = s - a

Ebenso kann man herleiten: |BX| = s - b und |CY| = s - c