
Symmetric Molecule-Based Feature Detector (SymFD, previously
CoShREM)
Gaussian mean width and ReLU singular values
Gabor-Steiner Equiangular Tight Frames
Musisep
BinderFinder
Equiangular Lines by Pillar Decomposition
Haar Wavelet-Based Perceptual Similarity Index (HaarPSI)
SymFD is a MATLAB toolbox providing methods for the detection and analysis of edges, ridges, and blobs in 2D images by utilizing the special symmetry properties of directionally sensitive 2D analyzing functions. Its predecessor, the Complex Shearlet-Based Edge and Ridge Measure (CoShREM) Toolbox, can also be downloaded here.
The image of a monarch butterfly used in the examples below is part of the LIVE Image Quality Assessment Database. The shown results can be reproduced by calling the respective scripts in the 'Examples' folder in the SymFD toolbox.
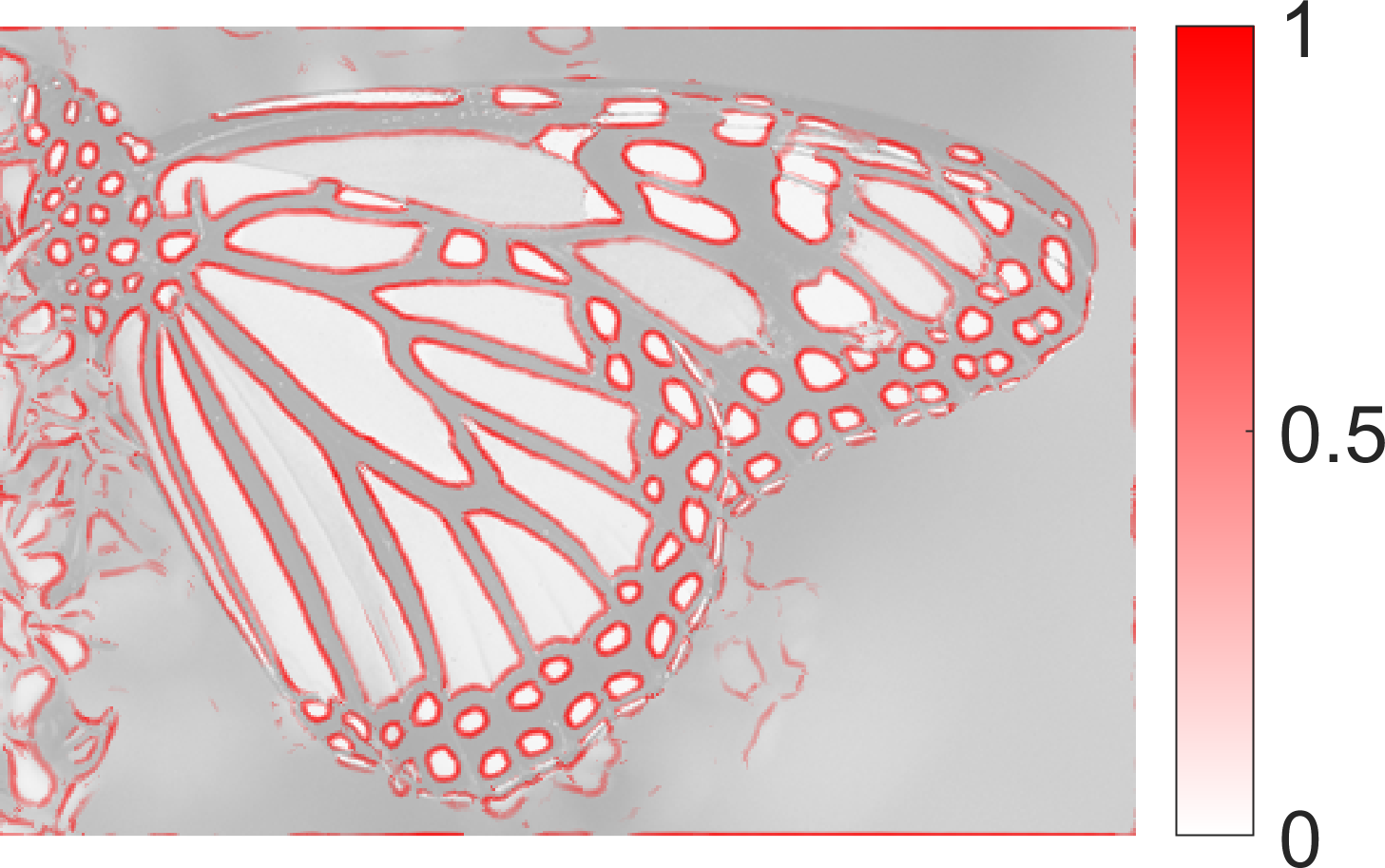 | 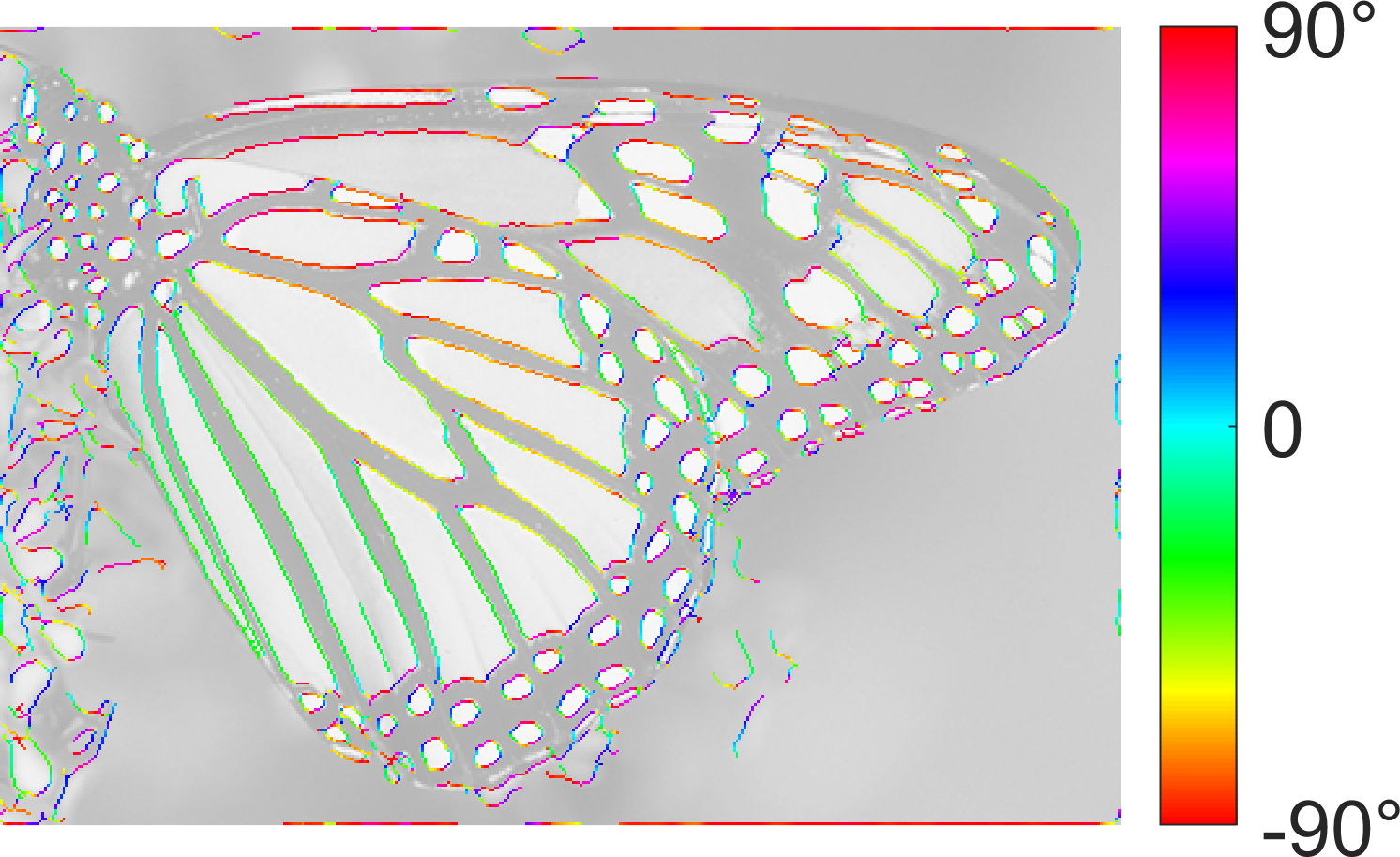 | 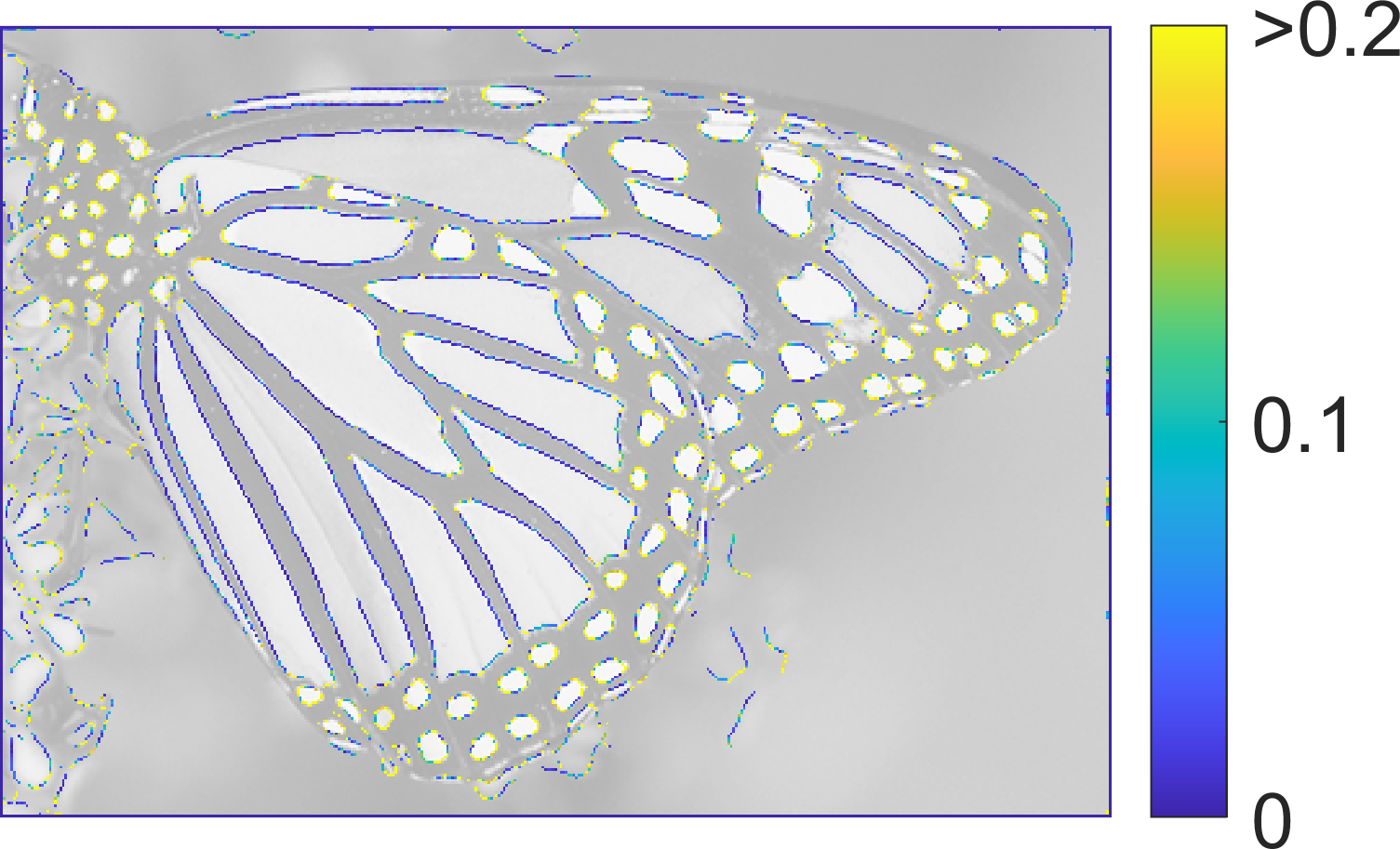 |
| SymFD Edge Measure | Tangent Directions | Curvature |
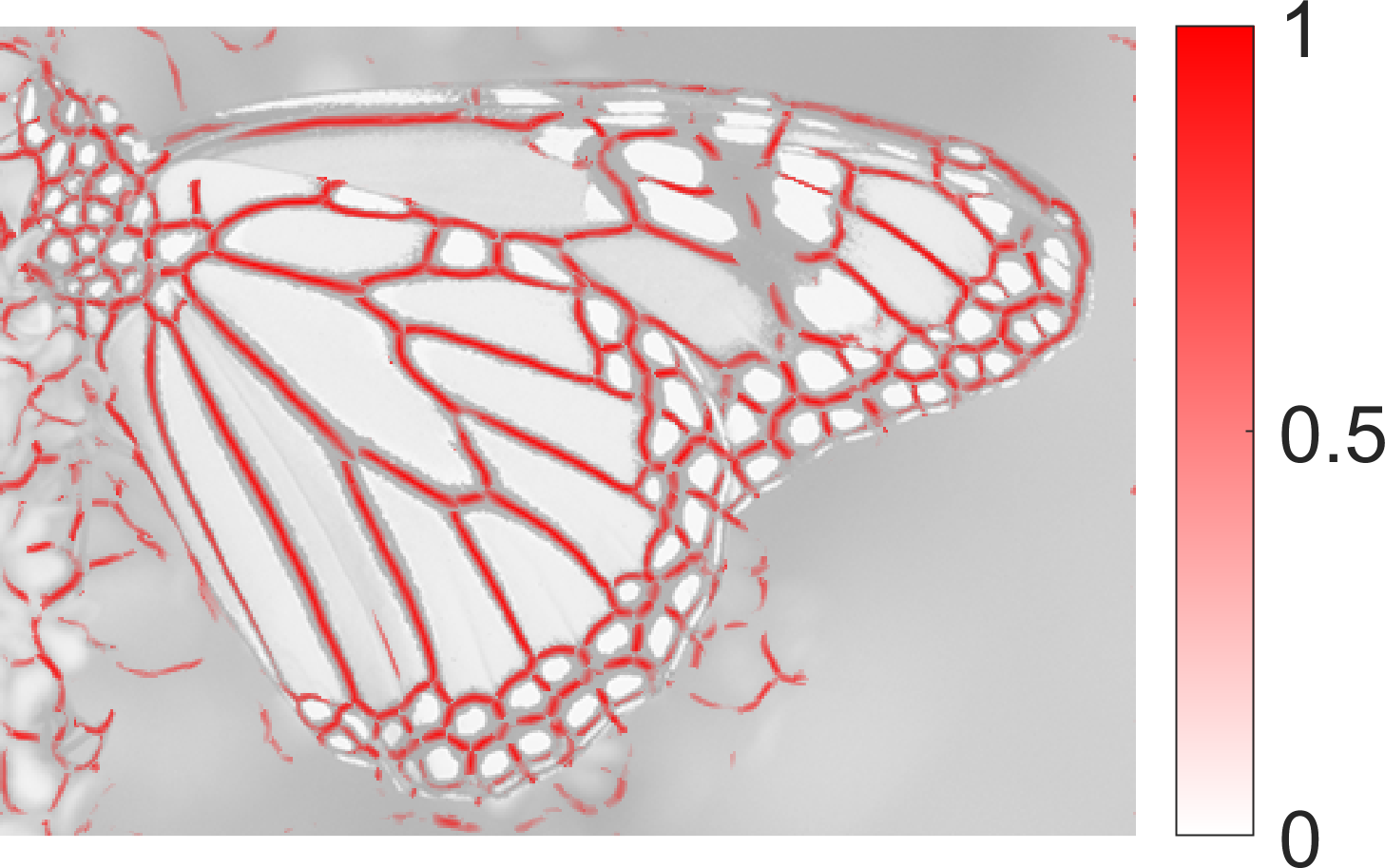 | 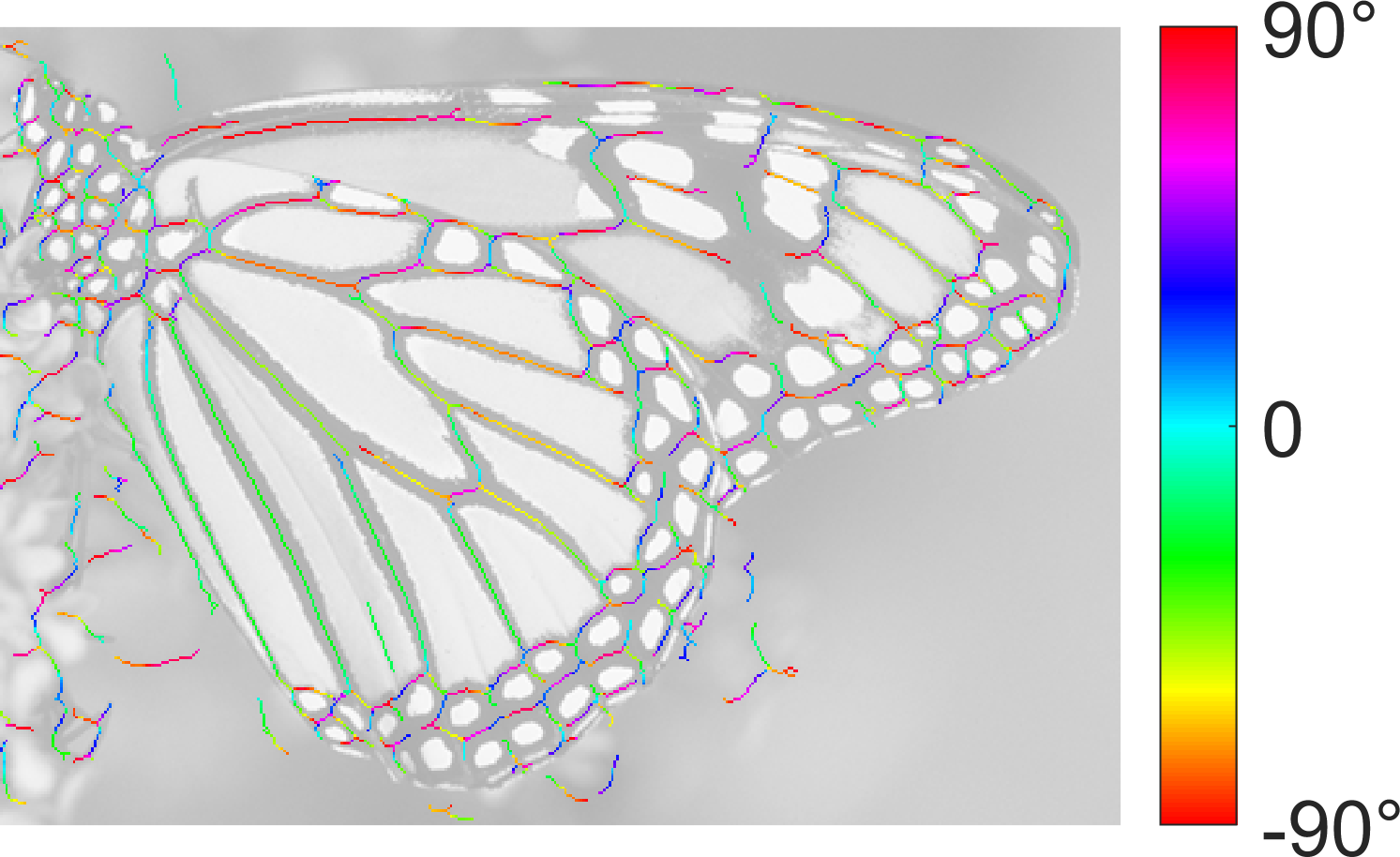 | 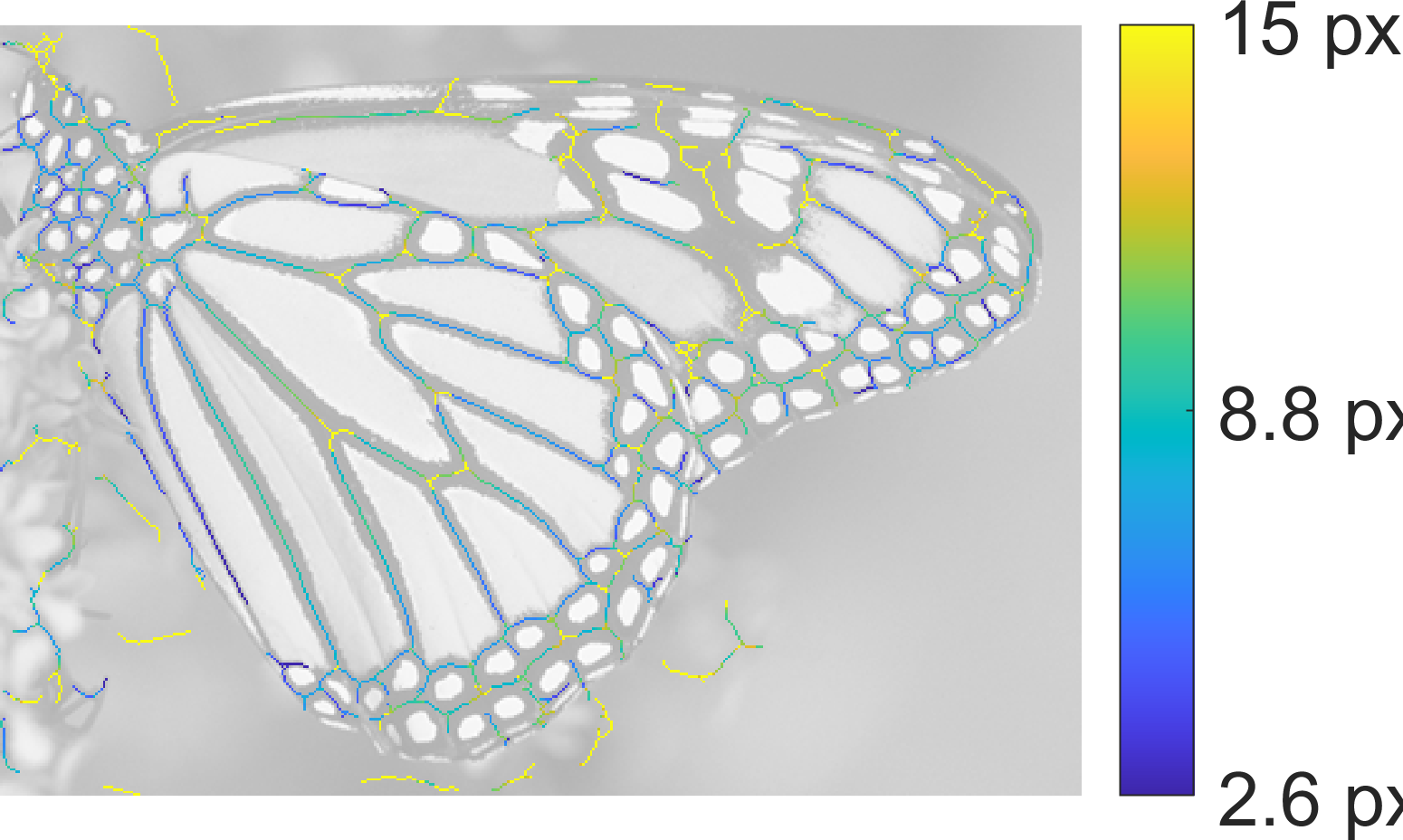 |
| SymFD Ridge Measure | Tangent Directions | Ridge Widths |
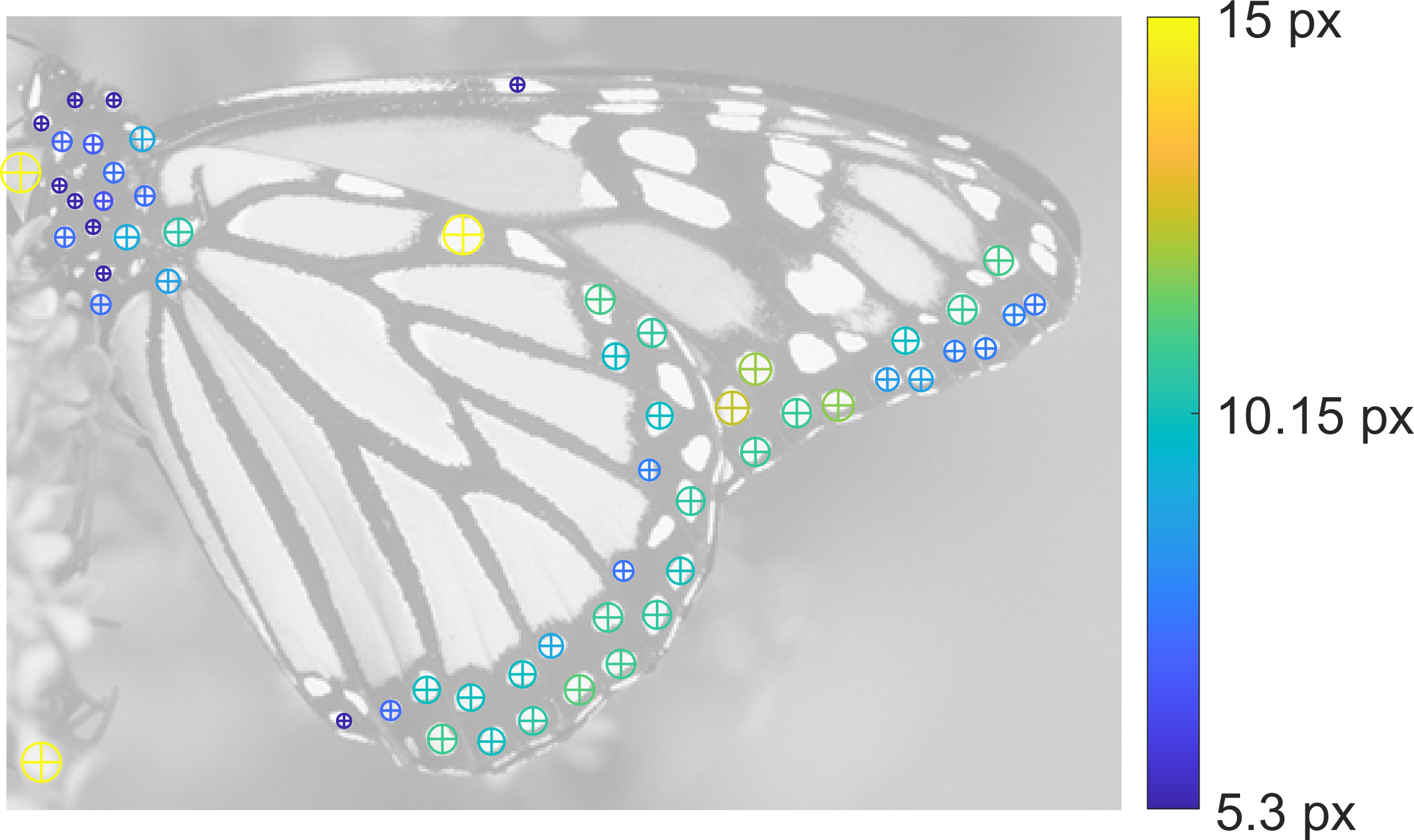 |
| Detected Blobs |
ReLU singular values are a generalization of singular values to maps
generated by the composition of an affine linear map and a component-wise
application of the rectified linear unit. For Python code to approximate
ReLU singular values, click here.
Gaussian mean width is a measure — in some sense — of
dimensionality of data. It can be used to differentiate between data that
is correctly or incorrectly classified in a trained discriminative neural
network. For Python code to calculate the Gaussian mean width of finite
data, click here.
For more information, see "Singular Values for ReLU Layers" by Soren
Dittmer, Emily J. King, and Peter Maass.
A Gabor-Steiner equiangular tight frame is generated as the orbit of a
special fiducial vector under a reducible projective representation of the
Weyl-Heisenburg group. As equiangular tight frames, Gabor-Steiner
equiangular tight frames satisfy a Parseval-like equality and span lines
which have constant pairwise angle. Further, Gabor-Steiner equiangular
tight frames have large numbers of embedded simplices. (See
BinderFinder below.)
A short Matlab code to generate Gabor-Steiner equiangular tight frames via
Weyl-Heisenburg groups over $\mathbb{Z}_m$ and $\mathbb{Z}_m \times
\mathbb{Z}_n$ for odd $m, n \geq 3$ may be downloaded
here.
For more information,
see "Optimal arrangements of classical and quantum states with limited
purity" by Bernhard Bodmann and Emily J. King, (PDF)
A Python program to blindly separate the contributions of different instruments in an audio recording via dictionary learning.
The algorithm uses a shift-invariant time-frequency representation that enables it to identify patterns of peaks in the spectrum corresponding to sounds of musical instruments regardless of pitch. Further refinement via non-linear optimization makes it independent of the tuning of the instruments and incorporates inharmonicity. Reasonability of the representation is ensured by a sparsity condition.
For the training of the dictionary, we use a modified version of ADAM, which is a state-of-the-art stochastic gradient descent algorithm.
These are the separation results for the 8th piece from the 12 Basset Horn Duos by Wolfgang A. Mozart (KV 487) in an arrangement by Alberto Gomez Gomez (license: CC BY-NC-SA 3.0) for two recorders, played on acoustic soprano recorder and violin:
A preprint describing the algorithm is available on arXiv, and the code is on GitHub (also refer to the API documentation). In order to reproduce the results, it must be run on the test data (ZIP).
Download the code here: BinderFinder.m
For more information, see "Equiangular tight frames that contain regular simplices" by Matthew Fickus, John Jasper, Emily J. King, and Dustin G. Mixon. (PDF)
By combining the pillar decomposition of Lemmens and Seidel 1973 with the semidefinite programming approach of Bachoc and Vallentin 2008 and Barg and Yu 2014 and further arguments from combinatorics and linear algebra, one is able to prove lower upper bounds on the size of sets of equiangular lines in various dimensions which are in some cases significantly better than the previously known bounds.
For more information, see the paper "New Upper Bounds for Equiangular Lines by Pillar Decomposition" by Emily J. King and Xiaoxian Tang, PDF. The code and supplementary materials may be found here.
The Haar wavelet-based perceptual similarity index (HaarPSI) is a similarity measure for images that aims to correctly assess the perceptual similarity between two images with respect to a human viewer.
In most practical situations, images and videos can neither be compressed nor transmitted without introducing distortions that will eventually be perceived by a human observer. Vice versa, most applications of image and video restoration techniques, such as inpainting or denoising, aim to enhance the quality of experience of human viewers. Correctly predicting the similarity of an image with an undistorted reference image, as subjectively experienced by a human viewer, can thus lead to significant improvements in any transmission, compression, or restoration system.
For more information and downloads please visit www.haarpsi.org. The HaarPSI is also available on github.