X6: Der Symmedian Point

Der Symmedian Point ist der Schnittpunkt der Symmediane des Dreiecks ABC.
Die Baryzentrischen Koordinaten sind a2 : b2 : c2.

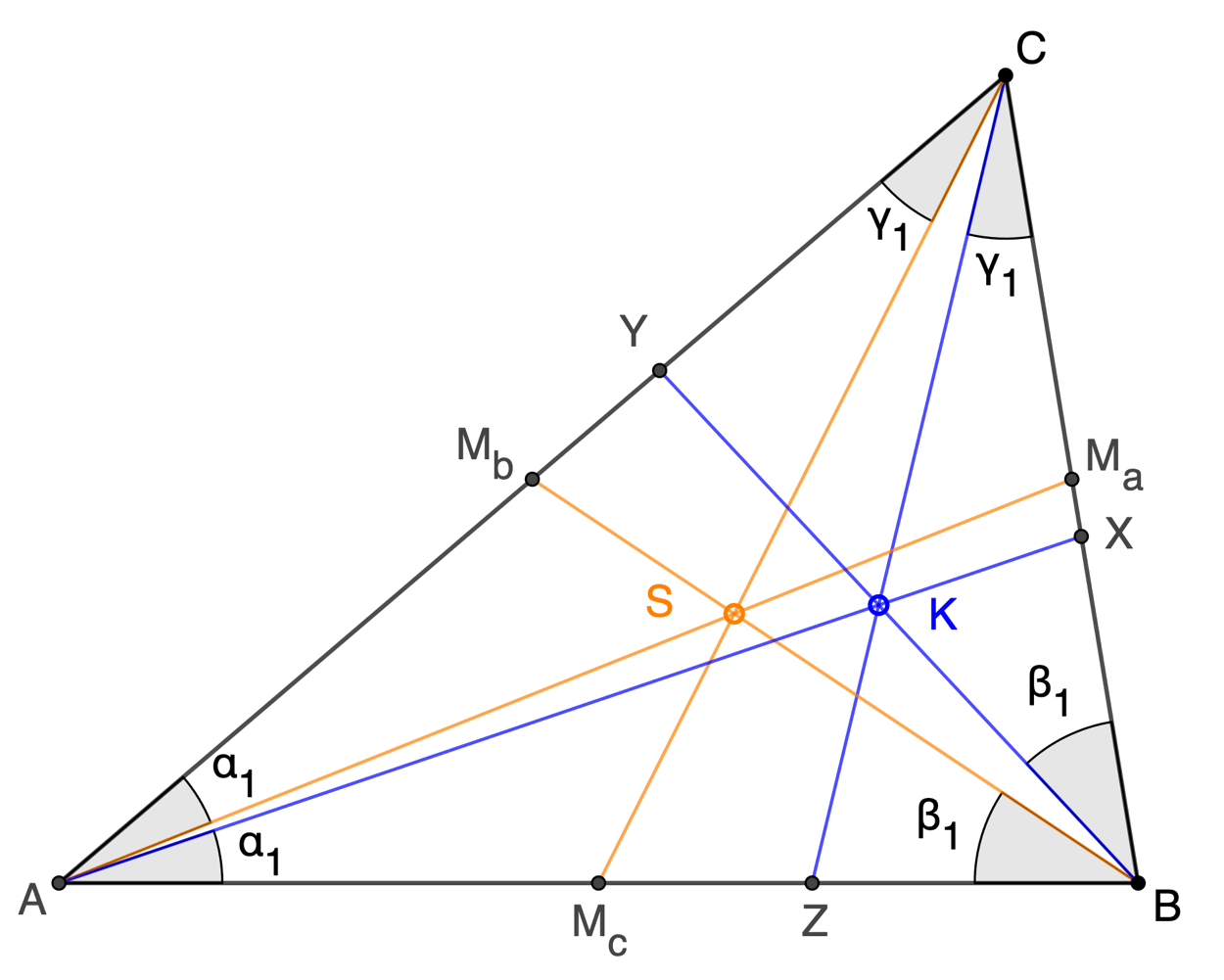
Der Symmedian Point, auch als Grebepunkt oder Lemoinepunkt bekannt, ist der isogonal konjugierte Punkt
zum Schwerpunkt des Dreiecks ABC. Er besitzt diverse bemerkenswerte Eigenschaften, die ihn zu einem
"Kronjuwel der modernen Geometrie" (Honsberger,1995) machen.

Einige Eigenschaften des Symmedian Points:

In jedem Dreieck ABC mit dem Symmedian Point K sind die Abstände des Punktes K zu den Seiten a,b und c proportional zu den Längen der Seiten a,b und c des Dreiecks ABC. Erläuterung und Beweis
Die Summe der Quadrate der Abstände eines Punktes P innerhalb des Dreiecks ABC zu den Seiten a,b und c ist genau dann minimal, wenn P mit dem Symmedian Point K des Dreiecks ABC übereinstimmt. Experimentaldatei
Der Symmedian Point des Dreiecks, das durch die drei Ankreismittelpunkte bestimmt wird, ist der Mittenpunkt des Ausgangsdreiecks ABC. Erläuterung und Beweis
Die Symmediane eines Dreiecks ABC schneiden den Umkreis des Dreiecks in den drei Punkten D,E und F. Der Symmedian Point K des Dreiecks ABC ist ebenfalls der Symmedian Point des Dreiecks DEF. Erläuterung
Im rechtwinkligen Dreieck ist der Symmedian Point K der Mittelpunkt der Höhe. Erläuterung und Beweis
Der Gergonnepunkt eines Dreiecks ist der Symmedian Point K des dazugehörigen Gergonnedreicks. Erläuterung und Beweis

zurück zur Liste der Dreieckszentren

Jan Kratschmer, R.Albers erstellt mit GeoGebra