Satz:
In einem Dreieck gilt für jeden Punkt P: Die drei isogonal konjugierten Ecktransversalen zu den drei durch den Punkt P definierten Ecktransversalen schneiden sich in einem Punkt P'.

Beweis:
Es ist zu zeigen, dass sich die Spiegeltransversalen in genau einem Punkt schneiden. Um dies zu beweisen, wird der Satz von Ceva in seiner trigonometrischen Form angewendet.

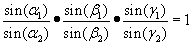
Da es sich beim Satz von Ceva um eine Äquivalenz handelt, muss man nur noch zeigen, dass die obige Gleichung gilt und kann daraus folgern, dass sich die Ecktransversalen in einem Dreieck in einem Punkt schneiden.

Für die Ecktransversalen durch den Punkt P gilt (linkes Dreieck) nach dem Satz von Ceva (trigonometrische Form):

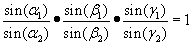
Bei den isogonal konjugierten Ecktransversalen sind die Winkel zu den Dreiecksseiten vertauscht (rechtes Dreieck). Dadurch ist das Verhältniss der Teilwinkel:

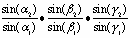
Diese Verhältnisse sind der Kehrwert der linken Seite der obigen Gleichung. Also gilt:

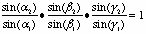
Folglich gilt nach der Umkehrung des Satzes von Ceva, dass sich die drei isogonal konjugierten Ecktransversalen in einem Punkt schneiden (rechtes Dreieck, Punkt P').

Definition: P' heißt der zu P isogonal konjugierte Punkt.

Folgerung: P ist der zu P' isogonal konjugierte Punkt. Man sagt daher auch, dass P und P' zueinander isogonal konjugiert sind.

Jan Kratschmer, Reimund Albers erstellt mit GeoGebra