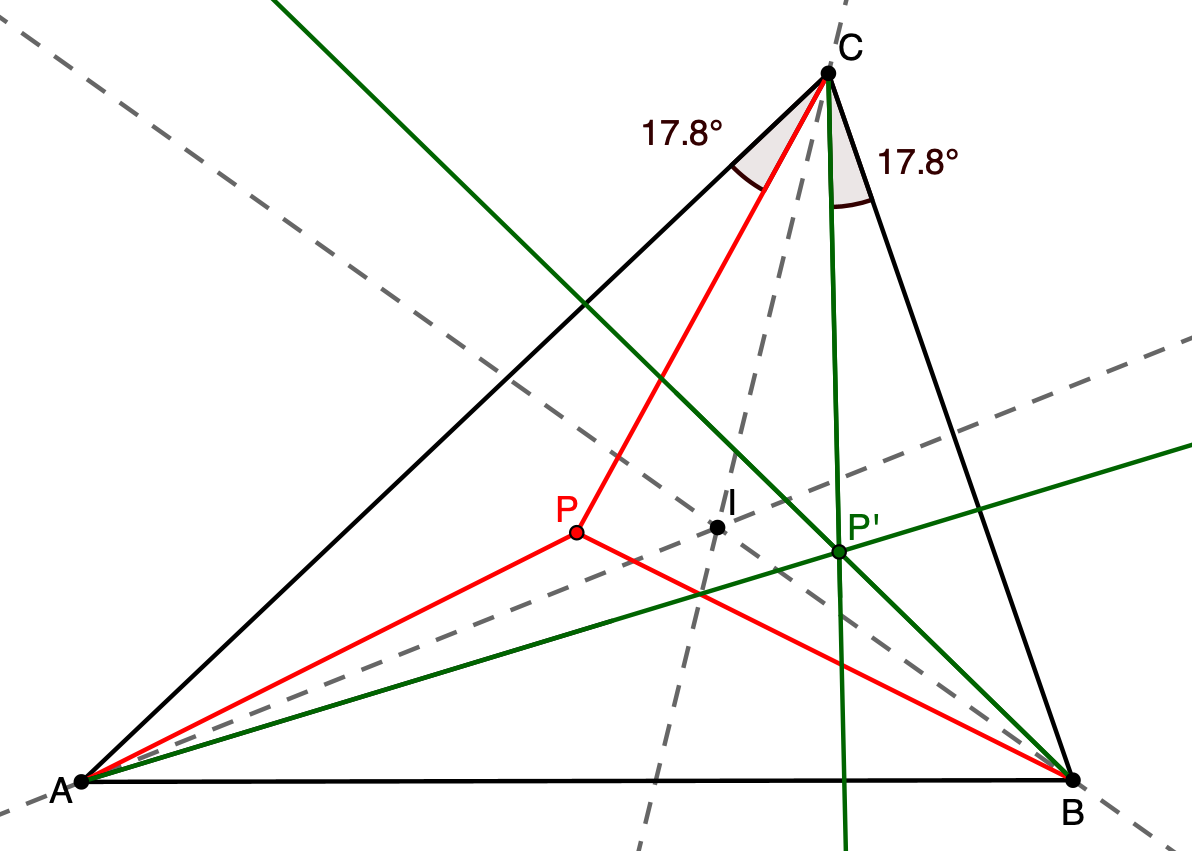
Man spiegelt die Ecktransversalen durch den Punkt P an
den zugehörigen Winkelhalbierenden (in der Abbildung
gestrichelt dargestellt) Die Spiegelbilder sind die
isogonal konjugierten Ecktransversalen, die sich in einem
Punkt P' schneiden. P' ist der isogonal konjugierte Punkt
zu P.
Beweis
Betrachten wir die Spiegelung an der Winkelhalbierenden des Winkels γ. Die Gerade AC wird auf die Gerade BC abgebildet und die Gerade PC auf die Gerade P'C. Spiegelungen sind winkeltreu, somit ist die Gerade PC isogonal konjugiert zur Geraden P'C. Analoges gilt für die anderen beiden Ecktransversalen durch P.
Da sich die drei isogonal konjugierte Ecktransversalen in
einem Punkt schneiden, muss P' der zu P isogonal
konjugierte Punkt sein.
Jan Kratschmer, R.Albers, erstellt mit GeoGebra