Gegeben ist ein Dreieck ABC und ein beliebiger Punkt P, zu dem der isogonal konjugierte Punkt P' konstruiert werden soll.

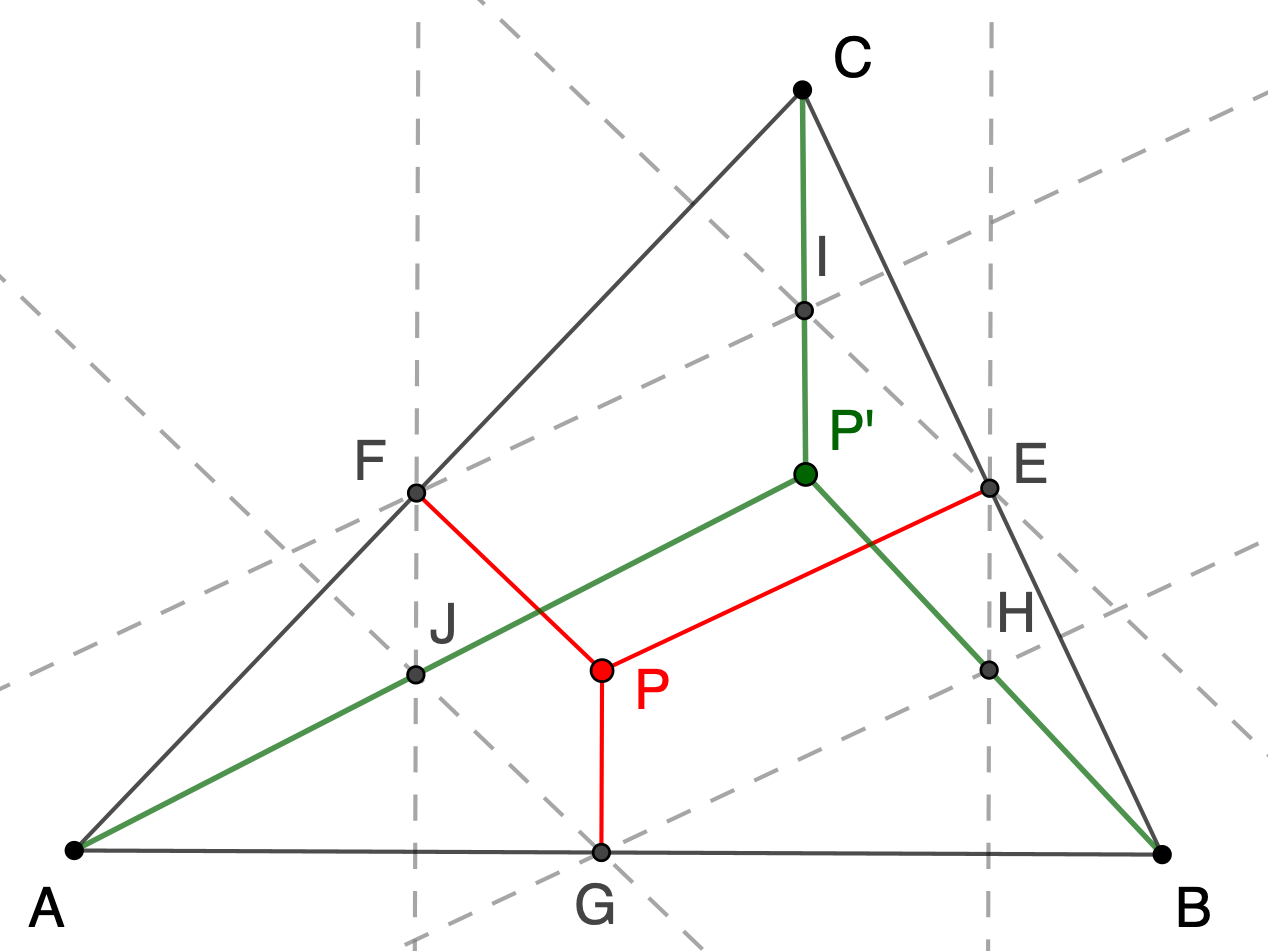
Konstruktionsbeschreibung
Konstruiere zu P die Senkrechten zu den Dreiecksseiten. Die Fußpunkte seien E,F und G.
Durch die Punkte E,F und G werden jeweils Parallelen (gestrichelt) zu den Loten PE, PF und PG konstruiert.
H ist der Schnittpunkt, der P, G und E zu einem Parallelogramm ergänzt. Analog ergeben sich die Schnittpunkte I (Parallelogramm PEIF) und J (Parallelogramm PFJG) (siehe Abbildung). Die Ecktransversalen AJ, BH und CI schneiden sich in einem Punkt P'. Dieser ist der isogonal konjugierte Punkt zu P.

Beweis

Um zu beweisen, dass P' bei dieser Konstruktion der isogonal konjugierte Punkt zu P ist, muß man zeigen, dass H,I und J auf Ecktransversalen liegen, die den gleichen Winkel zwischen den Dreiecksseiten einschließen wie die der Ecktransversalen durch P.

 

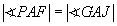
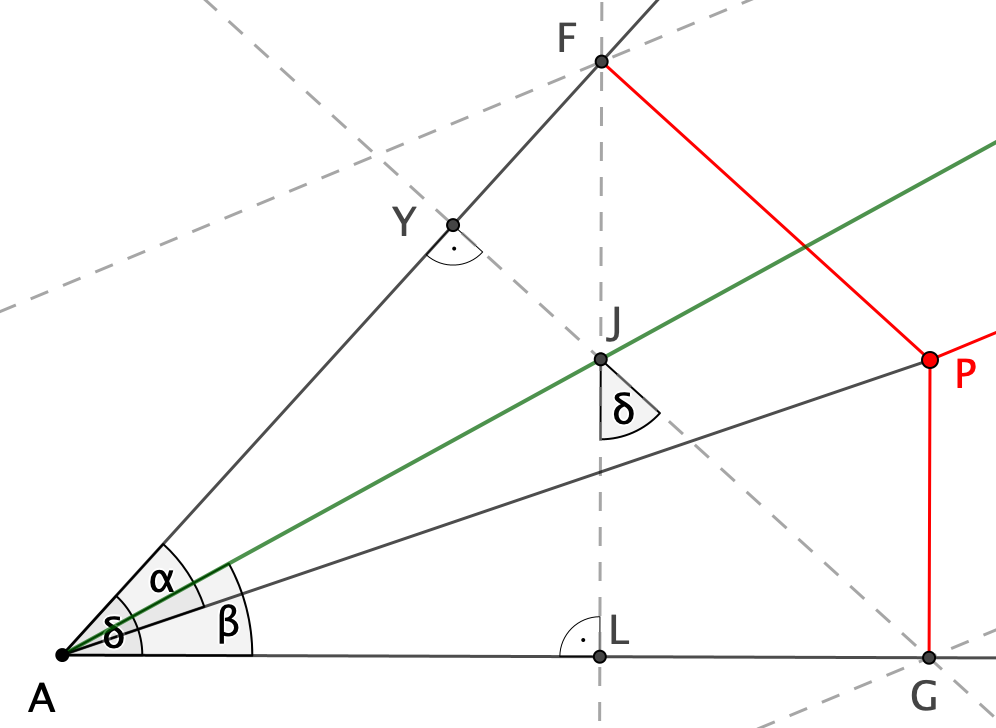
Für die nachfolgende Herleitung werden folgende Bezeichnungen eingeführt (siehe auch Abbildung):
α = Winkel PAF, β = Winkel GAJ , δ = Winkel GAF
Der Schnittpunkt von FJ mit AG sei L, der von GJ mit AF sei Y.
Zur Vereinfachung wird gesetzt. Dann ist und .

Im rechtwinkligen Dreieck ALF mit der Hypotenuse und dem Winkel δ bei A gilt
  und
Außerdem gilt im Dreieck ALJ: .

Da die Gerade GY senkrecht auf AC und die Gerade LF senkrecht auf AB steht, erhält man: .
Folglich gilt im Dreieck JLG also

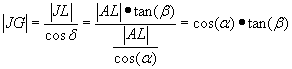
Setzt man nun (gegenüberliegende Seiten im Parallelogramm), dann erhält man
, also .

Da beide Winkel aus dem Intervall sind, folgt daraus.

Zur Lagebeziehung: Der Beweis wurde durchgeführt für den Fall α + β > δ.
Für den Fall α + β < δ ergibt sich ein ganz ähnlicher Beweis.

Zurück

Jan Kratschmer, R.Albers, erstellt mit GeoGebra