Gegeben ist ein Dreieck ABC und ein beliebiger Punkt P,
zu dem der isogonal konjugierte Punkt P' konstruiert
werden soll.
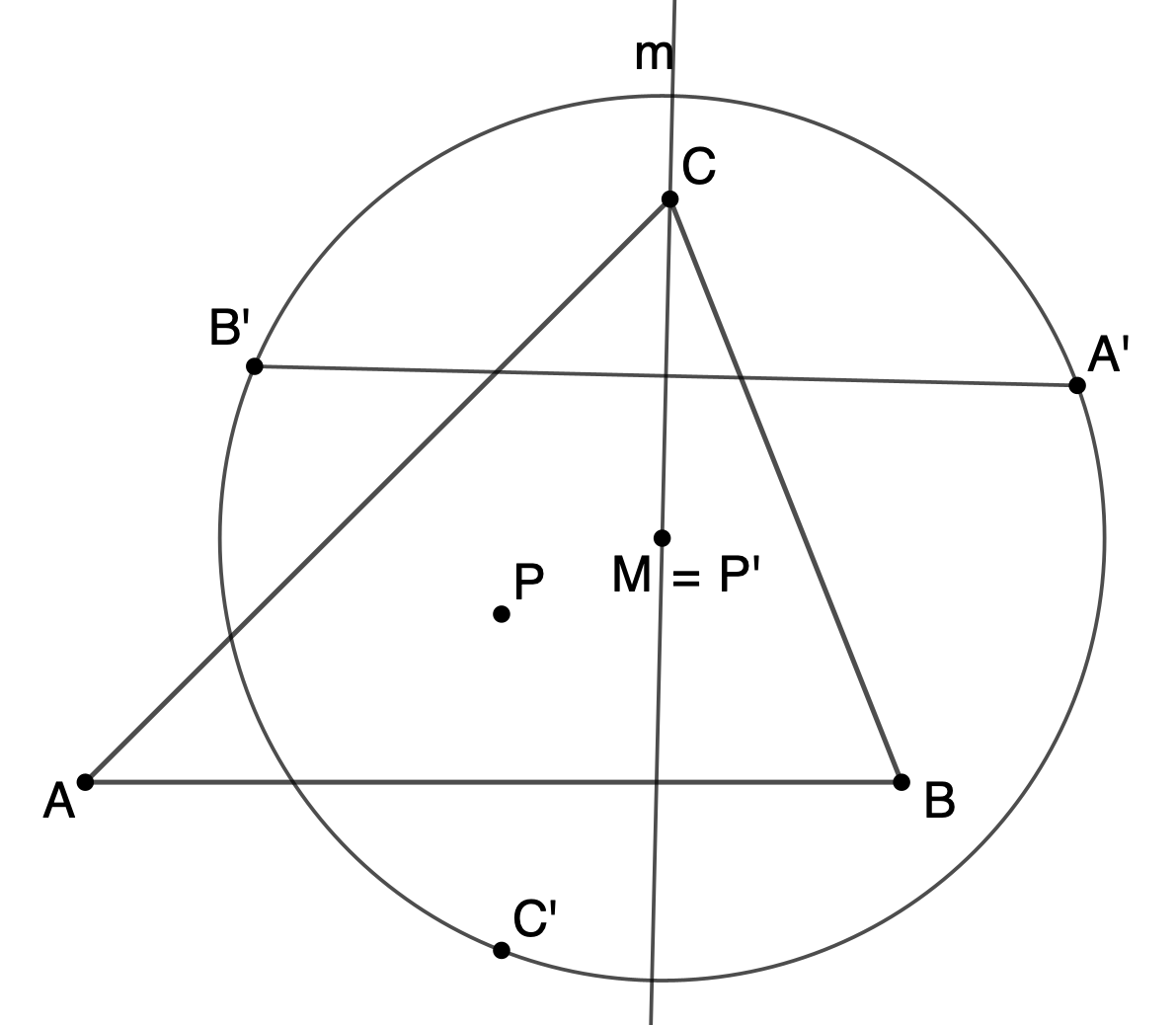
Konstruktionsbeschreibung
Der Punkt P wird an den drei Dreiecksseiten gespiegelt,
somit entstehen die Punkte A', B' und C'. Zum Dreieck
A'B'C' wird der Umkreismittelpunkt konstruiert. Er ist der
isogonal konjugierte Punkt P' zu P.
Beweis
1. Teil:
zu zeigen: Die Mittelsenkrechte m der Strecke A'B' verläuft durch den Punkt C.
Der Punkt B' entsteht durch Spiegelung des Punktes P an
der Geraden AC, ebenso entsteht der Punkt A' durch
Spiegelung des Punktes P an der Geraden BC. Die Gerade m
ist Mittelsenkrechte zu A'B'.
Aufgrund der Spiegelung an AC ist|PC| = |B'C| und wegen
der Spiegelung an BC ist |PC| = |A'C| und somit ist das
Dreieck A'B'C gleichschenklig.
Aus der Gleichschenkligkeit des Dreiecks A'B'C folgt, dass
die Gerade m als Mittelsenkrechte der Basis durch den
Punkt C verläuft.
2. Teil:
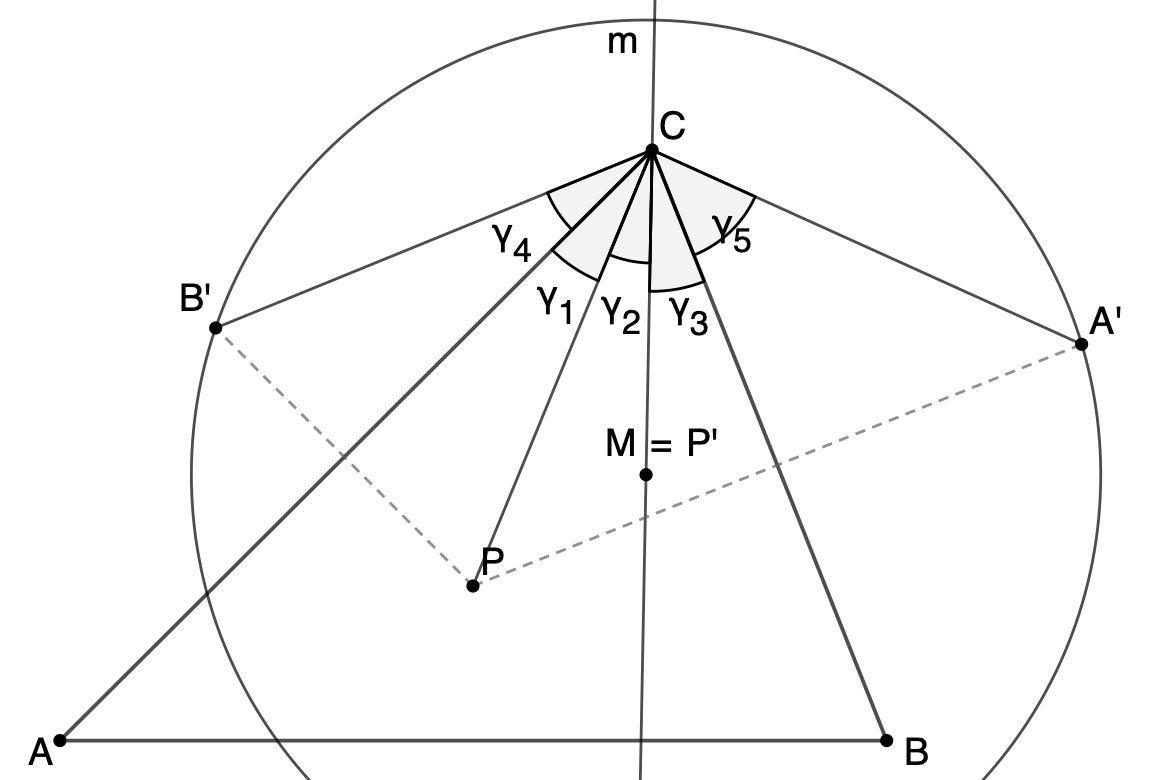
Die Geraden PC und m zerteilen γ in die drei Teilwinkel 
.
Zu zeigen ist: 
(d.h. m ist die isogonal
konjugierte Ecktransversale zu PC)
und 
weitere Winkel mit Scheitelpunkt C wie
eingezeichnet. 1. Das Dreieck PCB' ist gleichschenklig:
2. Das Dreieck A'CP ist gleichschenklig:
3. Das Dreieck A'CB' ist gleichschenklig:
Durch Einsetzen der ersten beiden Gleichungen in die
dritte Gleichung erhält man:
=> 
=> .
Für andere Lagebeziehungen von P zu m ergibt sich ein
ganz analoger Beweis.
Jan Kratschmer, R.Albers, erstellt mit GeoGebra