Satz von Ceva

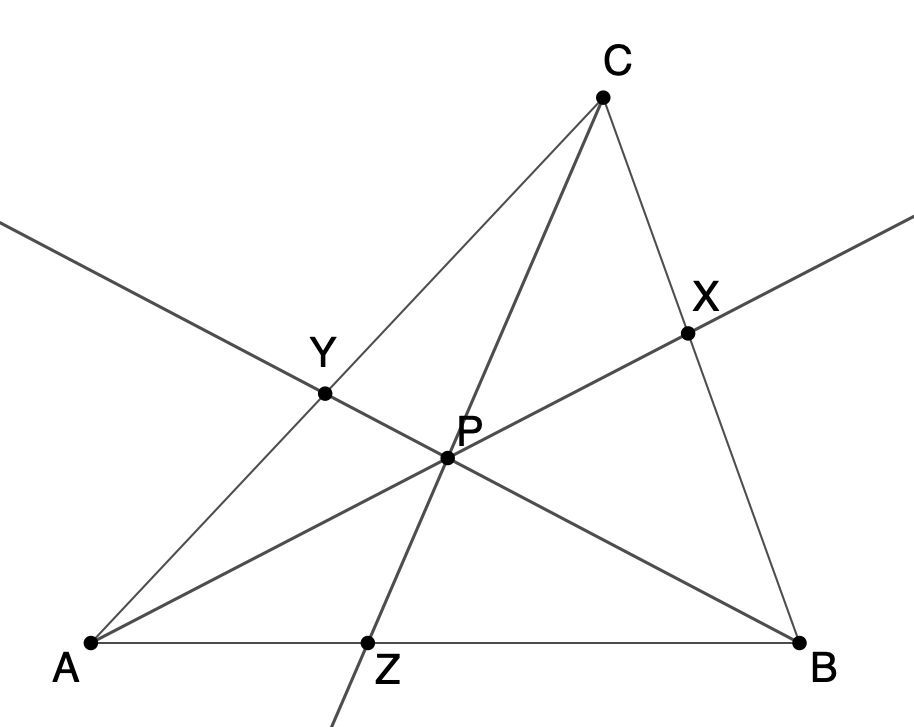
Die drei durch einen Punkt P verlaufenden Ecktransversalen scheiden die gegenüber liegenden Seiten in den Punkten X, Y und Z. Dann hat das Produkt der Quotienten, bestehend aus den entstandenen Teilstrecken der Dreiecksseiten, immer den Wert 1:


Merkregel: Man läuft um das Dreieck herum und schreibt die dabei durchlaufenen Teilstrecken auf die Brüche.

Die Umkehrung des Satzes von Ceva lautet:

Gilt für drei Ecktransversalen die Gleichung



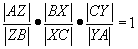
so schneiden sich die Ecktransversalen in einem Punkt.

Satz von Ceva in trigonometrischer Darstellung

Mithilfe des Sinussatzes: 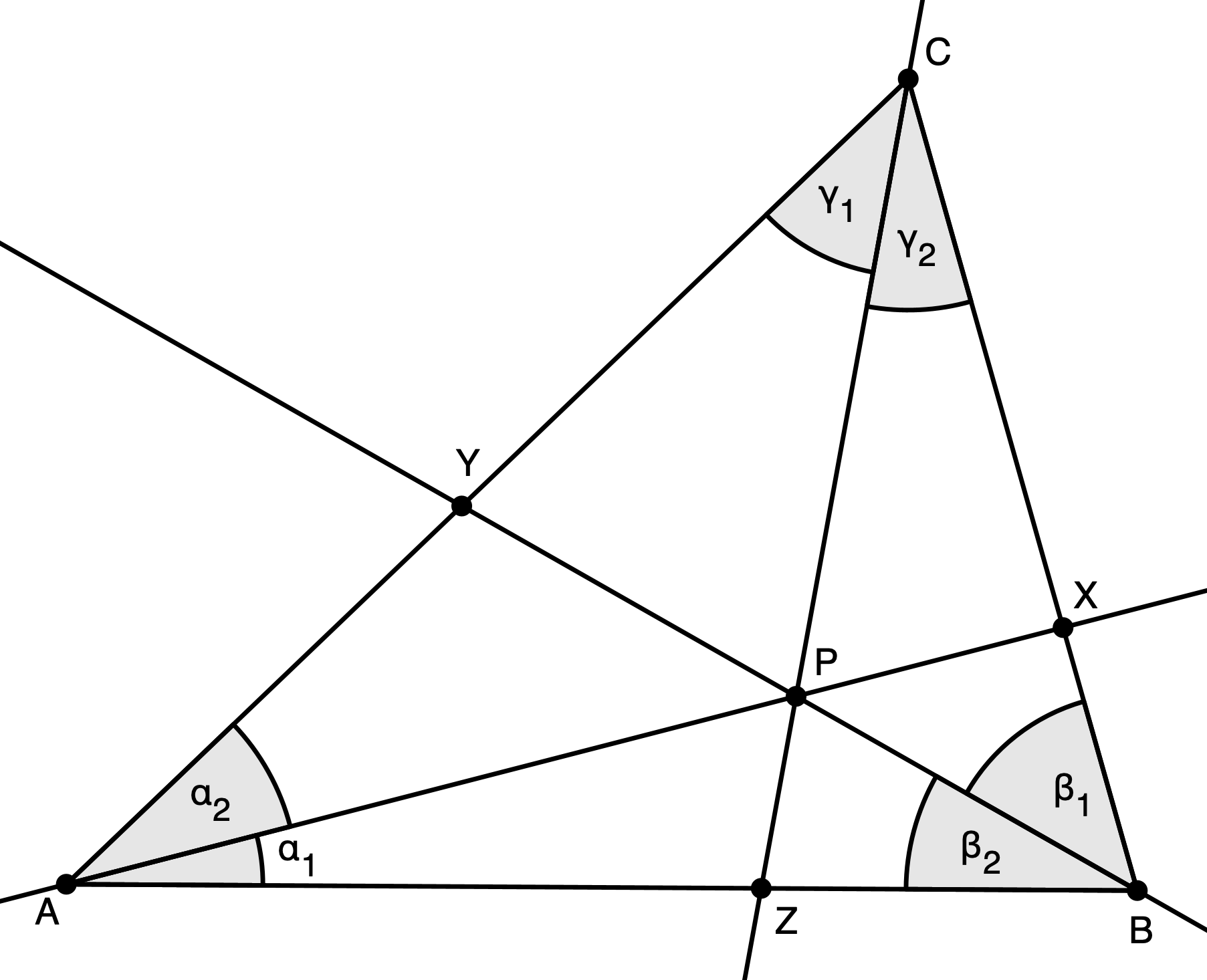, lässt sich eine Beziehung zwischen den Teilwinkeln, die durch die Ecktransversalen entstehen, und den Gesamtwinkeln herstellen:


, ,

, ,

Diese sechs Gleichungen werden nach den Größen umgestellt, die in der ursprünglichen Version des Satzes von Ceva vorkommen, z.B.:

oder

Formt man alles sechs Gleichungen um, und setzt diese dann in die ursprüngliche Gleichung des Satzes von Ceva ein, erhält man folgende Gleichung:


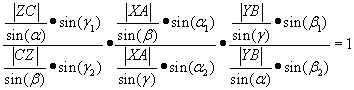
Nach Kürzen erhält man die trigonometrische Darstellung des Satzes von Ceva:


Zurück

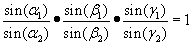
Jan Kratschmer, R. Albers Erstellt mit GeoGebra