Mittenpunkt

Der Symmedian Point des Dreiecks, das durch die drei Ankreismittelpunkte bestimmt wird,
ist der Mittenpunkt des Ausgangsdreiecks ABC.



Erläuterung
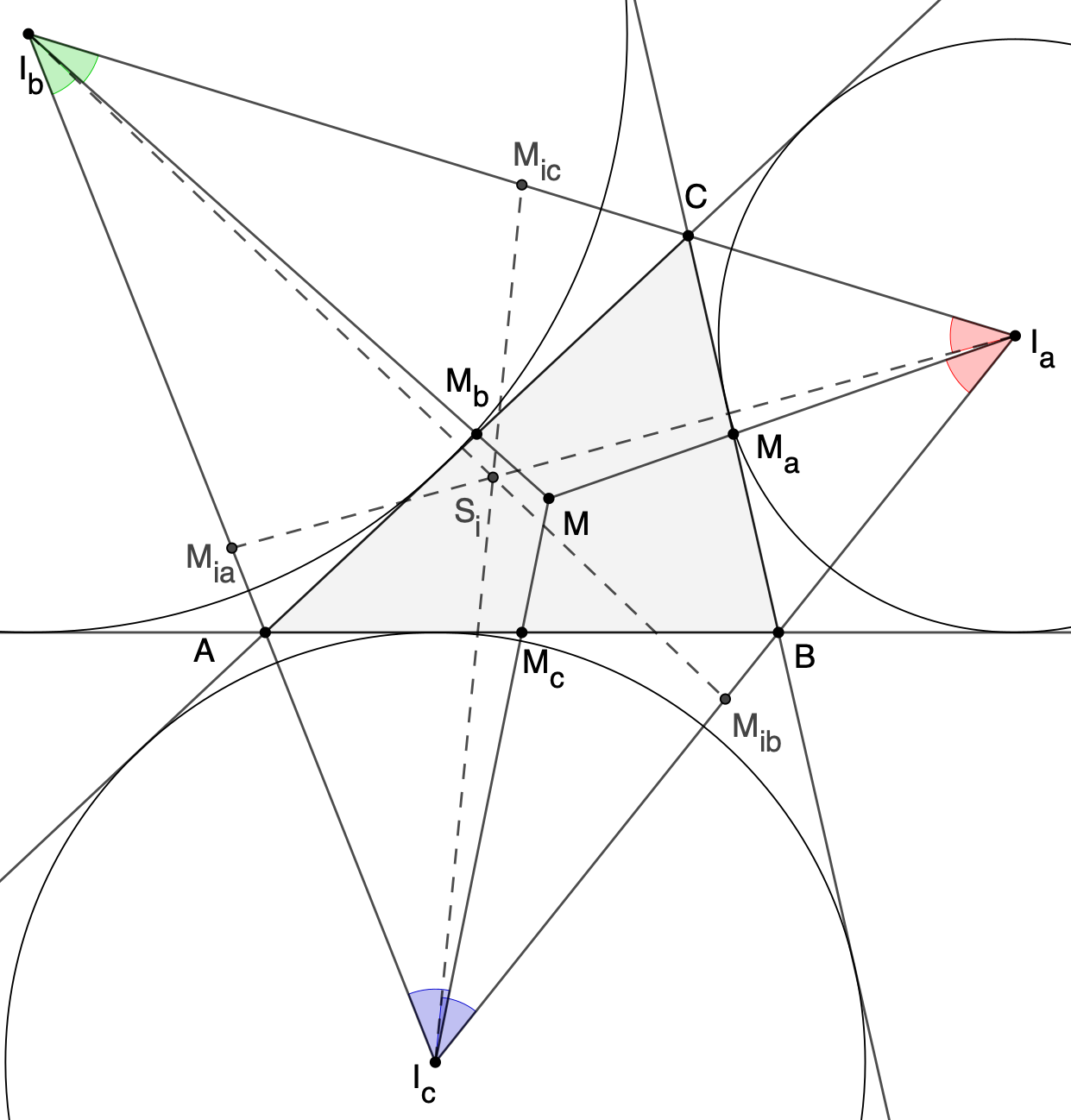
Gegeben ist das Dreieck ABC. Zu diesem Dreieck werden die drei Ankreise konstruiert. Die dabei entstandenen drei Ankreismittelpunkte Ia, Ib und Ic bilden ein zweites, größeres Dreieck. Konstruiert man den Symmedian Point dieses Dreiecks, so ist dieser Punkt gleichzeitig der Mittenpunkt des Dreiecks ABC. D.h. er ist der Schnittpunkt der Geraden durch jeweils einen Ankreismittelpunkt und dem zugehörigen Seitenmittelpunkt des Ausgangsdreiecks ABC.
In der obigen Abbildung ist M der Mittenpunkt des Dreiecks ABC und Si der Schwerpunkt des Dreiecks IaIbIc. Dann bedeutet die Aussage des Satzes letztlich, dass im Dreieck IaIbIc der Winkel zwischen einer Ecktransversalen durch M und einer Dreiecksseite so groß ist wie die der zwischen der zugehörigen Schwerelinie (gestrichelt) und der anderen Dreiecksseite. In der Abbildung oben ist es durch gleiche Farben der Winkel angedeutet.

Beweis
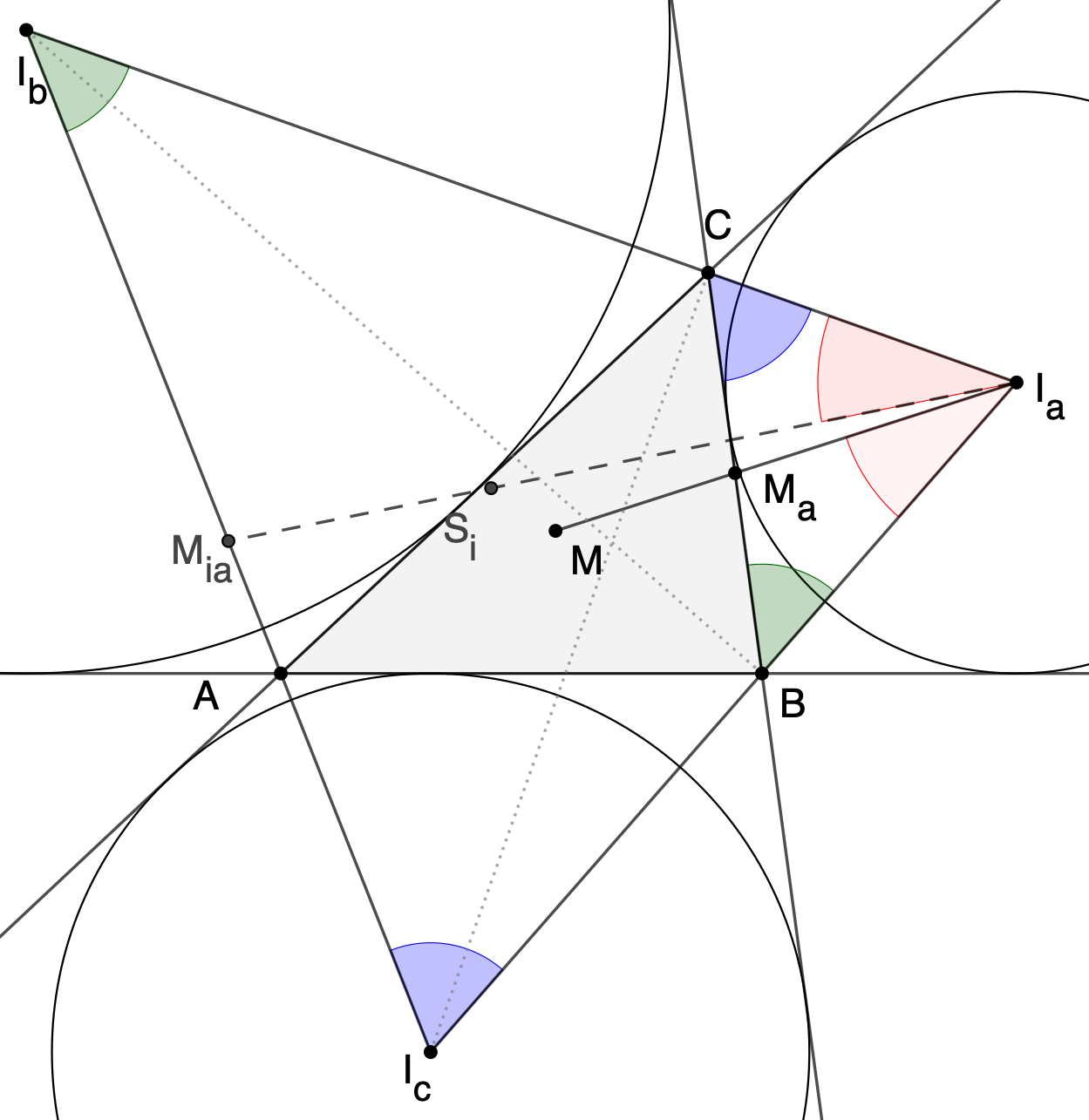Der Beweis wird exemplarisch gezeigt für die Gerade IaMa zum Mittenpunkt und IaMia zum Schwerpunkt.

Behauptung
|∠MaIaB| = |∠CIaMia|
(in der Abbildung rechts rot markiert)

Ganz wesentlich für die Beweisführung ist, dass das Dreieck BIaC ähnlich ist zum Dreieck IaIbIc. Das ist eine allgemeine Eigenschaft des Höhenfußpunkt-dreiecks, kann hier aber auch explizit gezeigt werden.
IbB ist die Winkelhalbierende des Winkels β und Höhe im Dreieck IaIbIc.
Daher ist |∠IaBC|=90°−β2((|<I_aBC|=90°-\frac{β}{2}  (grün markiert).
Mit der gleichen Logik gilt dann
|∠BCIa|=90°−γ2|<BCI_a|=90°-\frac{γ}{2}  (blau markiert)
Dann ergibt sich mit der Winkelsumme im Dreieck BIaC : |∠CIaB|=90°−α2|<CI_aB|=90°-\frac{α}{2} .
Mit der gleichen Logik erhält man
|∠AIbC|=90°−β2|<AI_bC|=90°-\frac{β}{2}  (grün markiert) und
|∠BIcA|=90°−γ2|<BI_cA|=90°-\frac{γ}{2}  (blau markiert)
Also ist das Dreieck BIaC ähnlich ist zum Dreieck IaIbIc. Damit gibt es eine Ähnlichkeitsabbildung, die B auf Ib und C auf Ic abbildet und Ia auf sich. Da Ähnlichkeitsabbildungen Teilverhältnisse erhalten, wird Ma auf Mia abgebildet (Seitenmitten), folglich auch der Winkel ∠MaIaB auf den Winkel ∠IbIaMia. Und da Ähnlichkeitsabbildungen winkeltreu sind, sind beide Winkel gleich groß.

Zurück

Jan Kratschmer, R. Albers erstellt mit GeoGebra