In einem rechtwinkligen Dreieck ist der Symmedian Point K der Mittelpunkt der Höhe der Hypotenuse.

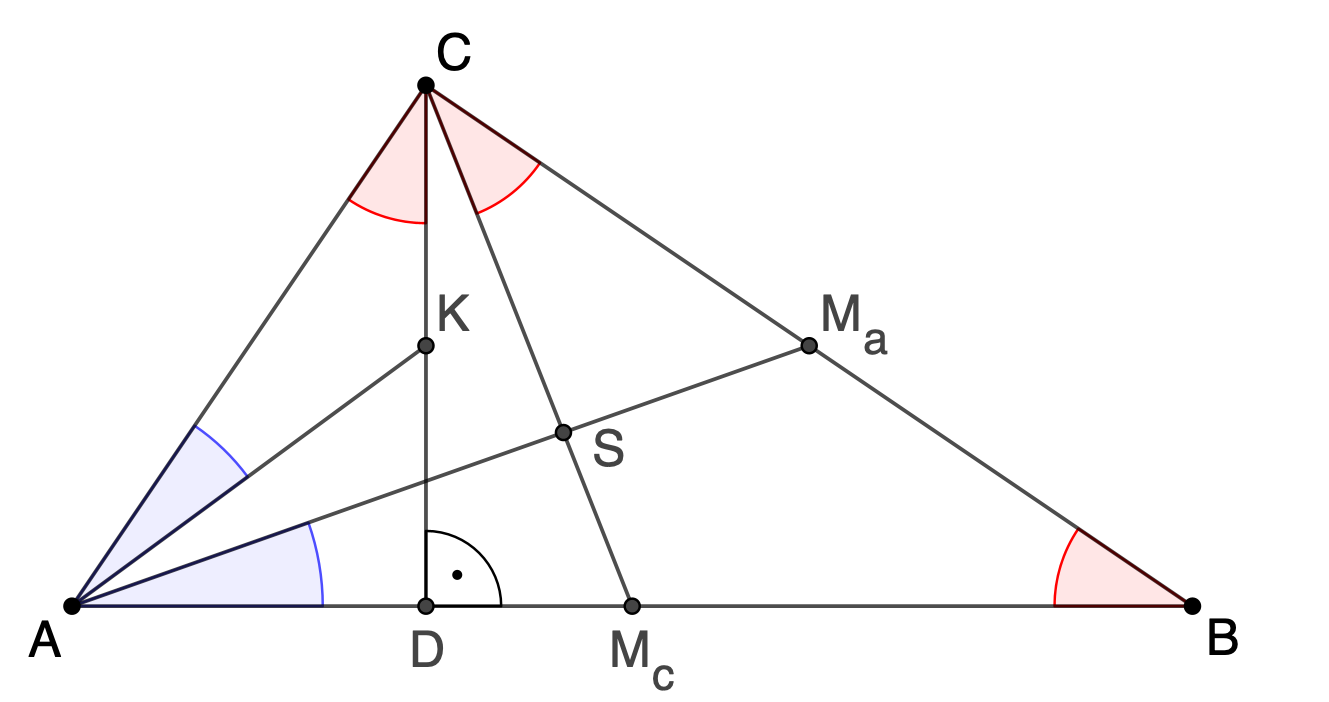
Beweis
Es muss gezeigt werden, dass die Seitenhalbierenden (Ecktransversalen durch den Schwerpunkt S) den gleichen Winkel zur Dreiecksseite einschließen wie die Ecktransversalen durch den Symmedian Point K. Das wird hier gezeigt für die Ecktransversalen durch A und C.
a) durch A (blaue Winkel)
Die Dreiecke ACD und ABC sind ähnlich. Also gibt es eine Ähnlichkeitsabbildung, die A auf sich, B auf C und C auf D abbildet. Da Ähnlichkeitsabbildungen das Teilungsverhältnis erhalten, wird der Mittelpunkt Ma der Seite BC auf den Mittelpunkt K der Seite CD abgebildet. Da Ähnlichkeitsabbildungen winkeltreu sind, gilt |∠KAC| = |∠BAMa|. Damit ist AK eine Symmediane des Dreiecks ABC.
b) durch C (rote Winkel)
Wie üblich sei |∠CBA| = β. Das Dreieck McBC igleichschenklig mit |CMc| = |McB|, da beide Radien des Thaleskreises sind. Also ist |∠McCB| = β. |∠CBA| = β ist der entsprechende Winkel zu ∠ACD in den ähnlichen Dreiecken ACD und ABC. Also gilt |∠ACD| = β. Damit ist CD ebenfalls eine Symmediane.
Damit ist K Schnitt zweier Symmediane, also der Symmedian Point.

Jan Kratschmer, R. Albers, erstellt mit GeoGebra