Gergonnepunkt

Der Gergonnepunkt eines Dreiecks ABC ist der Symmedian Point K des dazugehörigen Gergonnedreicks XYZ.



Erläuterung
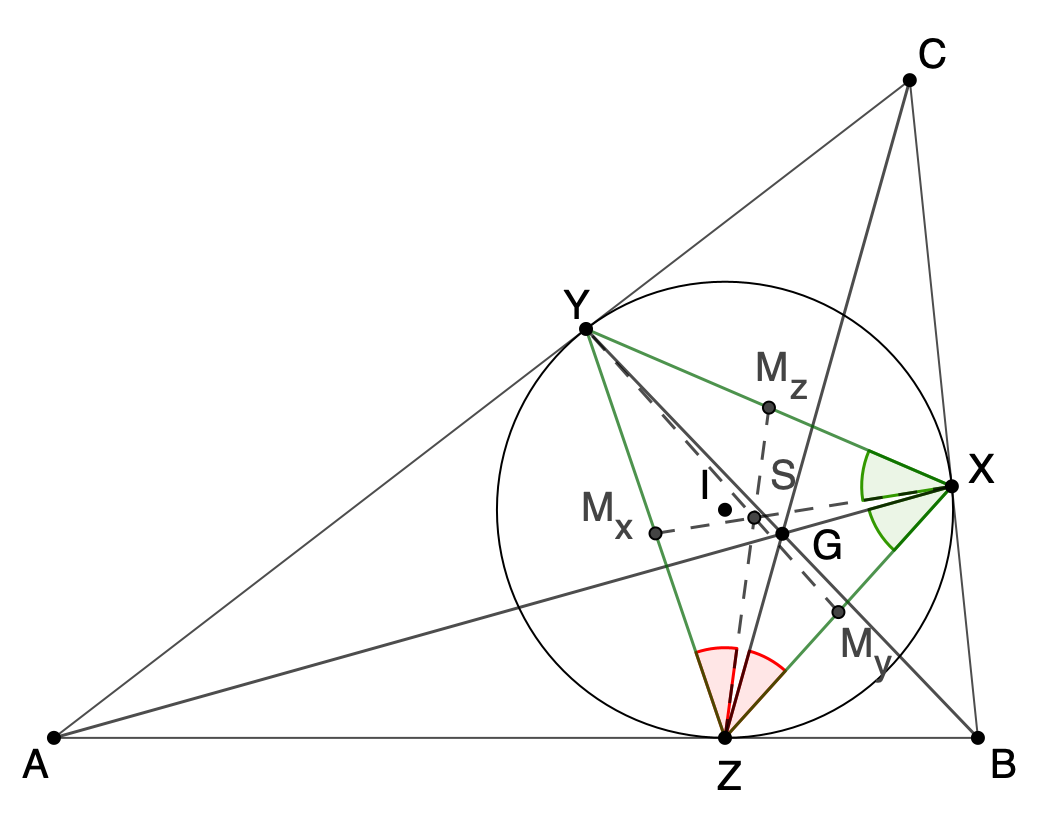
Im Dreieck ABC wird der Inkreis gezeichnet mit dem Mittelpunkt I und den Berührpunkten X, Y und Z. Die Ecktransversalen AX, BY und CZ schneiden sich in einem Punkt, dem Gergonnepunkt.
Das Dreieck, das durch die drei Berührpunkte XYZ gebildet wird, heißt Gergonnedreieck. In Bezug auf dieses sind AX, BY und CZ ebenfalls Ecktransversalen. Die Behauptung ist, dass diese Ecktransversalen Symmediane sind, also die isogonal konjugierten Ecktransversalen zu den Seitenhalbierenden (gestrichelt). S ist der Schwerpunkt des Dreiecks XYZ, Mx, My und Mz sind die Seitenmitten. Konkret bedeutet das, dass |∠XZG| =|∠SZY| (rot), |∠GXZ| =|∠YXS| (grün) und |∠GYX| =|∠ZYS| (nicht markiert).

Beweis

1. Schritt
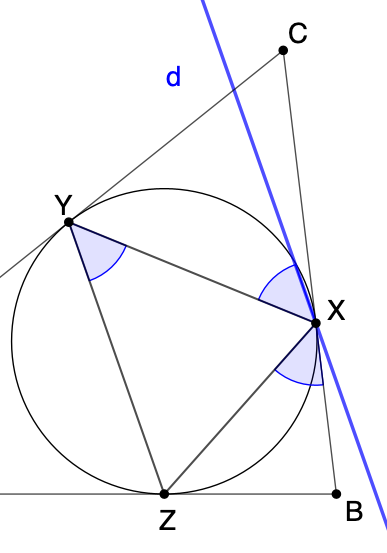
Zur Geraden BC wird die isogonal konjugierte Gerade konstruiert.
Der Winkel ∠ZXB ist Sehnen-Tangenten-Winkel zwischen der Sehne ZX und der Tangente BC. Folglich ist er so groß wie der Peripheriewinkel (bezüglich des Inkreises von ABC). Diese Winkelgröße wird in X an XY im Uhrzeigersinn angetragen. Das liefert die Gerade d, die isogonal konjugierte Gerade zu BC in Bezug auf das Dreieck XYZ, in der Abbildung rechts blau markiert.
Die Winkel mit dem Scheitelpunkt bei Y und bei X sind Wechselwinkel gleicher Größe. Folglich ist die Gerade d parallel zur Geraden YZ.


2. Schritt
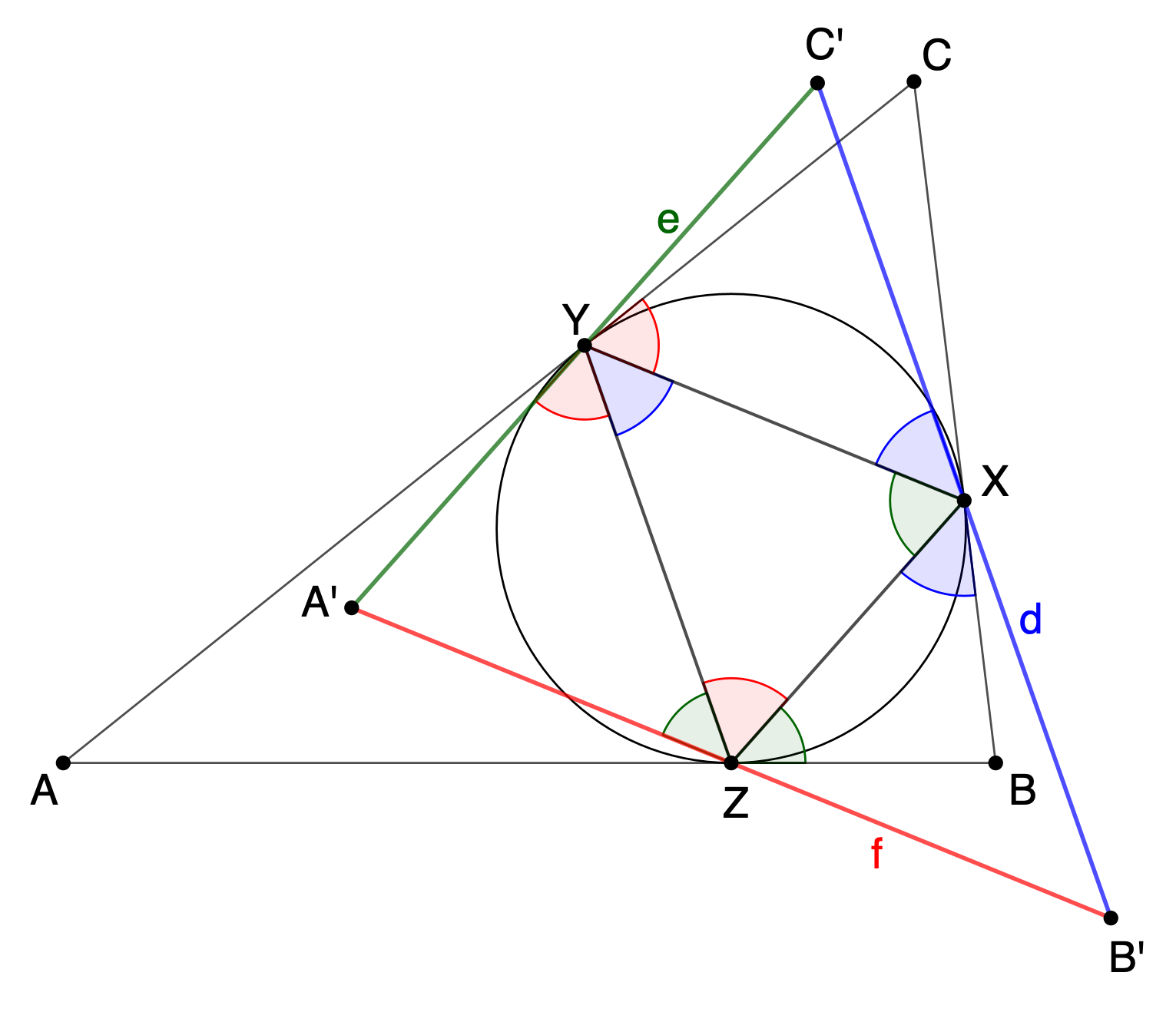
Mit der gleichen Logik wie in Schritt 1 ist die Parallele e zu XZ durch Y die isogonal konjugierte Gerade zu AC und die Parallele f zu XY durch Z die isogonal konjugierte Gerade zu AB.
In Bezug auf das Dreieck XYZ ist d die isogonal konjugierte Gerade zur Geraden durch C zur Ecke X und e ist die isogonal konjugierte Gerade zur Geraden durch C zur Ecke Y. Damit ist der Schnitt von d und e, der Punkt C',  der isogonal konjugierte Punkt von C in Bezug auf das Dreieck XYZ
In analoger Weise gilt das für den Punkt A', dem Schnitt von e und f und für den Punkt B' als Schnitt von f und d.



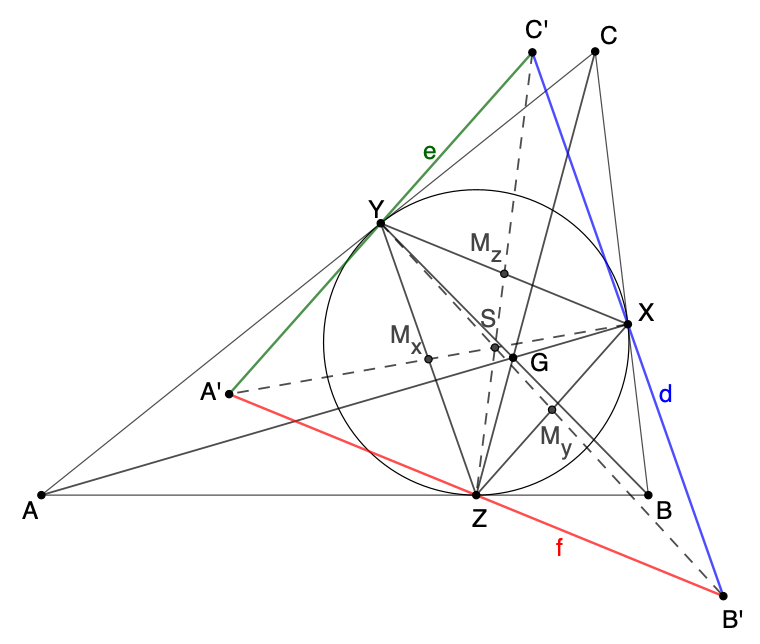3. Schritt
Da d||YZ und e||ZX und f||XY ist XYZ das Mittendreieck in Bezug auf das Dreieck A'B'C' . Damit ist z.B. das Viereck A'ZXY ein Parallelogramm, so dass A'X die Strecke YZ in deren Mittelpunkt Mx schneidet. Folglich ist A'X eine Seitenhalbierende für das Dreieck XYZ. Da A und A' isogonal konjugierte Punkte sind, sind auch die Geraden AX und A'X isogonal konjugiert. Also ist AX im Dreieck XYZ eine Symmediane (die zur Seitenhalbierenden XMx ).
Mit der gleichen Logik sind BY und CZ Symmediane. Alle drei schneiden sich im Symmedian Point des Dreiecks XYZ. Gleichzeitig sind AX, BY und CZ auch die Linien zum Gergonnepunkt des Dreiecks ABC.

Zurück

Jan Kratschmer, R. Albers erstellt mit GeoGebra