Gegeben ist ein Dreieck ABC und ein Punkt P. Die Abstände des Punktes P zu den Dreiecksseiten seien a', b' und c'. P ist genau dann der Symmedian Point K, wenn die Abstände a',b' und c' proportional zu den Längen der Seiten a,b und c des Dreiecks ABC sind.

Beweis:

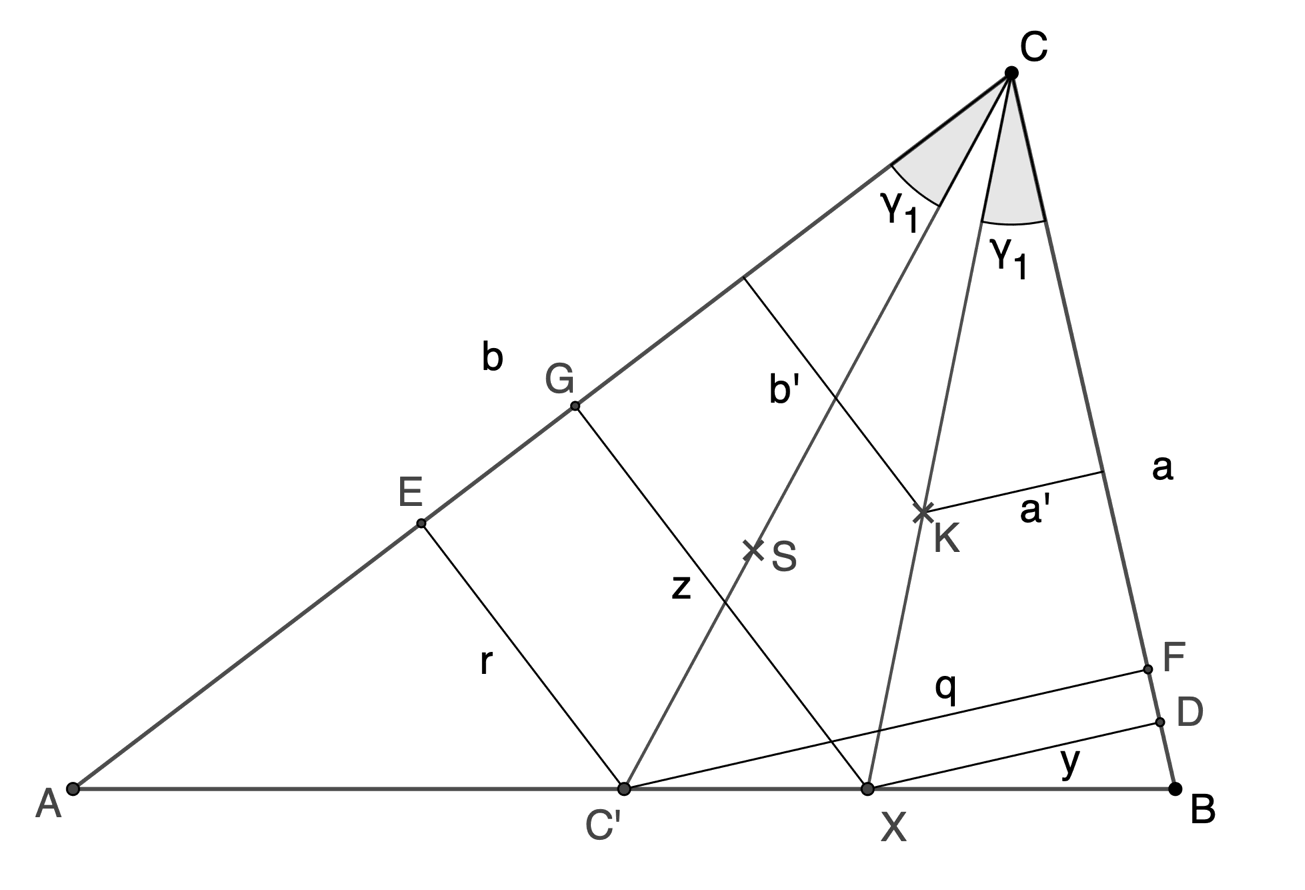
Die Ecktransversale CK trifft die Strecke AB in X. Der Abstand von X zu BC sei y, der zu AC z.
C' ist der Mittelpunkt der Strecke AB, somit ist CC' die Seitenhalbierende von C, auf der der Schwerpunkt S liegt.
Die Strecken r und q sind ebenfalls Abstände.

K ist Symmedian Point => a': b': c' = a : b : c.
Wir zeigen als Beispiel .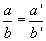

Nach dem 2. Strahlensatz mit Zentrum C gilt: 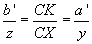. Daraus folgt 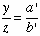. (1)
Da CC' Seitenhalbierende ist, sind die Flächen der Dreiecke AC'C und C'BC gleich groß. Also gilt: .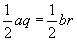

Daraus folgt dass 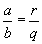ist. (2)

Da das Dreieck CXD ähnlich zu Dreieck CC'E ist (da ja K der isogonal konjugierte Punkt zu S ist), folgt .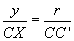

Analog sind die Dreiecke CC'F und CXG ählich, also 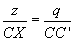, also ist 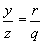. (3)

Durch Gleichsetzen von (2) und (3) erhält man 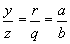. Die Kombination mit (1) liefert: .
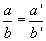Analog zeigt man die weiteren Beziehungen: , ...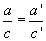

2.Teil:

a': b': c' = a : b : c => K ist Symmedian Point

Wähle K so, dass 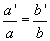ist.  Dann folgt nach zentrischer Streckung mit Zentrum C: 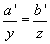und somit ist 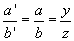. (4)

Nun wird zur Ecktransversalen CX die isogonal konjugierte konstruiert. Sie schneidet AB in C'. Es ist nun zu zeigen, dass C' die Mitte von AB ist, die isogonal konjugierte Ecktransversale also die Seitenhalbierende ist.
Das Lot von C' auf AC hat den Fußpunkt E.

Nach Konstruktion folgt dass die Dreiecke CXD und CC'E ähnlich sind und somit gilt: 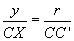und .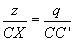
Daraus folgt 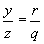und mit (4) ist 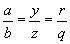. Jetzt sehen wir, dass 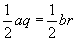ist und CC' somit die Fläche des

Dreiecks ABC halbiert. Daraus folgt dass C' der Mittelpunkt von AB ist und CC' somit Seitenhalbierende ist.

Gemäß der Konstruktion von CC' folgt, dass CK Symmediane durch C ist.
Analog zeigt man die Symmediane durch A und B.

Jan Kratschmer, R.Albers erstellt mit GeoGebra