Der Mittelpunkt des Umkreises ist der Schnittpunkt der
drei Mittelsenkrechten.
Die baryzentrischen Koordinaten sind ![]()
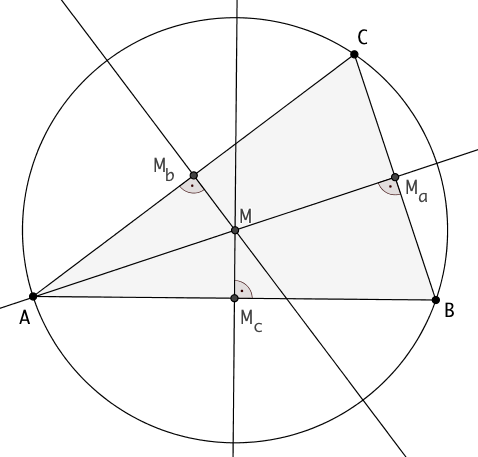
Definition der Mittelsenkrechten
Satz
Die drei Mittelsenkrechten eines Dreiecks schneiden sich
in einem Punkt.
Er hat von den drei Eckpunkten die gleiche Entfernung und
ist daher der Mittelpunkt des Umkreises.
Sätze, die mit dem Umkreis in Zusammenhang stehen:
| Der Schwerpunkt (X2), Mittelpunkt des Umkreises (X3) und Höhenschnittpunkt (X4) liegen auf einer Geraden, der Eulergeraden. | Beweis |
| Die Wallace/Simson-Gerade | Erläuterung und Beweis |
R. Albers, erstellt mit GeoGebra