Die Wallace/Simson-Gerade

Satz
Gegeben sei ein Dreieck ABC und ein Punkt P. Man fällt von P die drei Lote auf die (verlängerten) Dreiecksseiten und erhält die Fußpunkte Fa, Fb und Fc.
P liegt auf dem Umkreis des Dreiecks ABC <==> Die drei Fußpunkte liegen auf einer Geraden

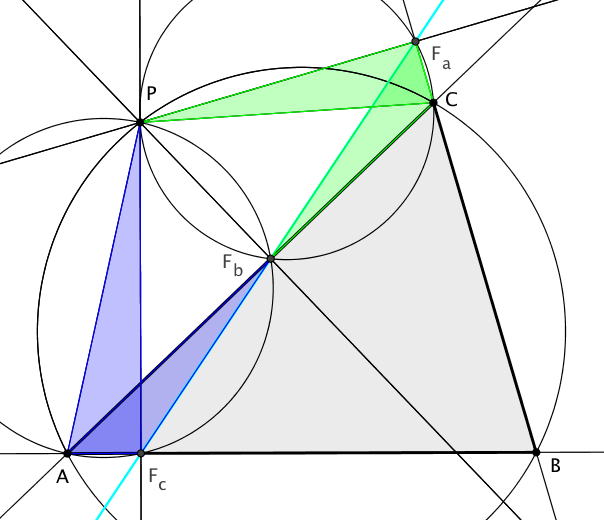
Beweis "==>"

Es sei P ein Punkt auf dem Umkreis. Wir zeigen zunächst den Beweis für den Fall, dass P auf dem Kreisbogen von C nach A liegt.
Das Viereck AFcFbP ist ein Sehnenviereck, da Fc und Fb auf dem Thaleskreis über der Strecke AP liegen (bei Fb und Fc sind rechte Winkel). Daraus folgt, dass die beiden Winkel APFc und AFbFc (blaue Winkel) als Peripheriewinkel über der Sehne AFc gleich groß sind.
Die analoge Argumentation gilt für das Viereck aus den Punkten C, Fa, P und Fb und die Winkel CPFa bzw. CFbFa (grüne Winkel). Da die vier Punkte P, A, B und C auf dem Umkreis liegen, ist der Winkel APC 180° - β. In dem Viereck FcBFaP gilt wegen der beiden rechten Winkel bei Fc und Fa, dass der Winkel FcPFa ebenfalls 180°- β ist. Daraus folgt, dass die blauen Winkel (Scheitel bei P bzw. Fb) so groß sind wie die grünen Winkel. Da A, Fb und C auf einer Geraden liegen, müssen dann auch Fa, Fb und Fc auf einer Geraden liegen.
q.e.d.

Analoge Argumentationen treffen zu, wenn P auf den Kreisbögen BC oder AB liegt.

"<=="

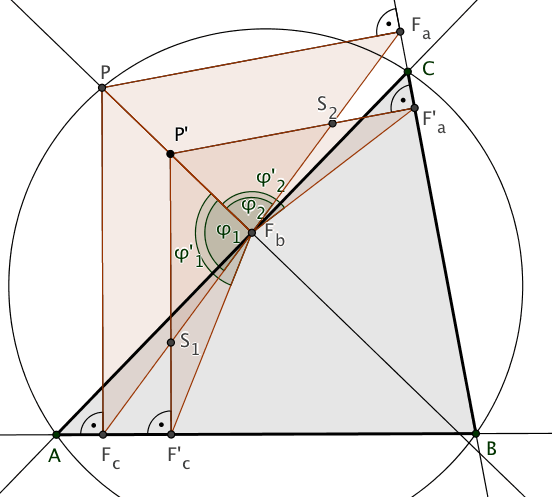
Der Beweis gilt zunächst für den Fall, dass ein Punkt P' innerhalb des Umkreises in dem Kreisabschnitt durch die Gerade AC liegt, der nicht die Dreiecksfläche enthält.

Das Lot von P' auf AC hat den Fußpunkt Fb und schneidet den Umkreis in P. Die Lote von P und P' auf AB und BC bilden die Fußpnkte Fc, F'c, Fa und F'a.
Laut dem oben gezeigten Beweis liegen Fa, Fb und Fc auf einer Geraden.
Sind |∠PFbFc| = φ1 und |∠FaFbP| = φ2, so gilt φ1+φ2 = 180°.
Nun liegt P' auf der Strecke FbP. Folglich schneidet das Lot von P' auf AB die Gerade FcFb im Punkt S1. Offensichtlich gilt |∠P'FbS1| = φ1. Wird nun die Strecke P'S1 verlängert zur Strecke P'F'c,
so gilt |∠P'FbF'c| = φ'1>φ1 (der längeren Strecke liegt der größere Winkel gegenüber).
Ebenso schneidet das Lot von P' auf BC die Gerade FbFa im Punkt S2. Offensichtlich gilt |∠S2FbP'| = φ2. Wird nun die Strecke P'S2 verlängert zur Strecke P'F'a, so gilt |∠F'aFbP'| = φ'2>φ2.
Dann ist der Winkel |∠F'aFbF'c| = φ'2+φ'1>φ2+φ1 = 180°. Folglich liegen die drei Fußpunkte F'a, F'b und F'c nicht auf einer Geraden.

Liegt nun P' in derselben Halbebene in Bezug auf AC, aber außerhalb des Umkreises des Dreiecks ABC, so ergeben sich S1 und S2 als Schnitte der Verlängerungen der Lote mit der Geraden FcFa. Die Strecke P'F'c ist dann kürzer als P'S1 bzw. P'F'a ist kürzer als P'S2.
Damit ist dann der Winkel |∠F'aFbF'c| = φ'2+φ'1<φ2+φ1 = 180°.

Bei anderen Lagen von P' sind die Punkte auszutauschen, damit sich eine analoge Argumentation ergibt.

Reimund Albers, erstellt mit GeoGebra