Beweis

Die drei Mittelsenkrechten eines Dreiecks schneiden sich in einem Punkt.

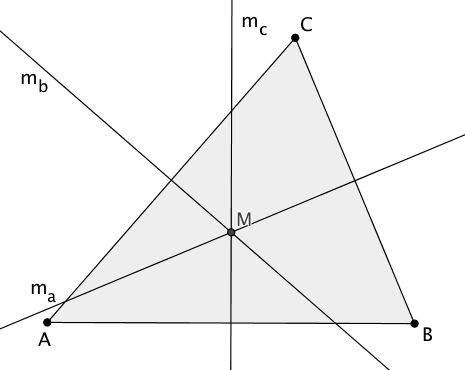
Es sei M der Schnittpunkt der beiden Mittelsenkrechten m_a und m_b.
Nach der Definition der Mittelsenkrechten gilt:
Da M auf m_a liegt, gilt: |MB| = |MC| .
Da M auf m_b liegt, gilt: |MC| = |MA| .
Also gilt auch: |MB| = |MA|. Das bedeutet aber, dass M auch auf der Mittelsenkrechten m_c liegt, also m_c durch M verläuft.

R. Albers, Erstellt mit GeoGebra