Dynamics of Automatic Control
| Arbeitsgruppe: | Ehemalige AAG Mathematische Modellierung komplexer Systeme |
| Leitung: | Prof. Dr. Sergey Dashkovskiy |
| Bearbeitung: |
Dr. Andrii Mironchenko
Dr. Lars Naujok |
| Projektförderung: | DFG (SFB 637 „Selbststeuerung logistischer Prozesse - Ein Paradigmenwechsel und seine Grenze“, Teilprojekt A5) |
| Projektpartner: |
Fachbereich Produktionstechnik, Universität Bremen Fachbereich Physik/Elektrotechnik, Universität Bremen Fachbereich Wirtschaftswissenschaft, Universität Bremen BIBA, Bremer Institut für Produktion und Logistik GmbH (BIBA) |
| Laufzeit: | 01.01.2004 - 31.12.2011 |
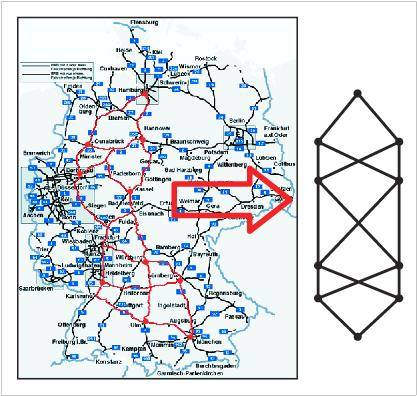
Der Sonderforschungsbereich SFB 637 befindet sich derzeit in der zweiten Förderphase. Er umfasst 16 Teil- und vier Transferprojekte, in denen Wissenschaftler aus vier Fachbereichen der Universität Bremen, der Jacobs University Bremen und der University of Wisconsin-Madison interdisziplinär zusammenarbeiten. Im Teilprojekt A5 untersucht die Arbeitsgruppe Mathematische Modellierung komplexer Systeme gemeinsam mit Wissenschaftlern des Bremer Instituts für Produktion und Logistik die Dynamik selbststeuernder logistischer Prozesse.
Die dynamische und strukturelle Komplexität logistischer Netzwerke verhindert zunehmend die Bereitstellung aller entscheidungsrelevanten Informationen für eine zentrale Planungs- und Steuerungsinstanz und erfordert deshalb adaptive logistische Prozesse mit der Fähigkeit zur Selbststeuerung. Mit Selbststeuerung wird die dezentrale Koordination autonomer logistischer Objekte in einer heterarchischen Organisationsstruktur bezeichnet.
In der zweiten SFB-Förderphase wurde der Betrachtungsgegenstand des Teilprojektes A5 von Produktionssystemen auf Produktionsnetze erweitert. Solche Netze bestehen aus geografisch verteilten Produktionsstandorten, die durch Transportwege verbunden sind. Neben der Betrachtung der zwei unterschiedlichen Ebenen (Produktionsstandort und -netz) werden Transportzeiten berücksichtigt.
Mithilfe der im Teilprojekt A5 entwickelten Selbststeuerungsstrategien steuern die logistischen Objekte, wie z.B. Material oder Aufträge, selbstständig durch ein Netzwerk. Dazu werden unter anderem die Auswirkungen der Anwendung von unterschiedlichen Selbststeuerungsstrategien hinsichtlich der Leistungsfähigkeit, Robustheit gegenüber Störungen und Stabilität analysiert. Beispielsweise wurde in einem Szenario eines Produktionsnetzes nachgewiesen, dass durch die Anwendung von Selbststeuerung die Lagerbestände der einzelnen Standorte unter schwankenden Material- bzw. Auftragseingängen harmonisiert werden, wie in der zweiten Abbildung zu erkennen ist.
Generelle Ziele des SFB-Teilprojektes sind die Modellierung von Produktionsnetzen, die Entwicklung und Integration unterschiedlicher Selbststeuerungsstrategien sowie die Analyse der Anwendung dieser Strategien und deren Dynamik in Produktionsnetzen. Es werden Modelle untersucht, die eine gute Approximation an das Systemverhalten liefern, um ein Werkzeug zur Simulation und konkreten Vorhersage der Dynamik von Transportprozessen zur Verfügung zu stellen, und es werden qualitative Aussagen über das Verhalten selbstgesteuerter Transportprozesse gewonnen, die ein allgemeines Verständnis der zu erwartenden Dynamik vermitteln.
Mathematisch werden Produktionsnetze mit Differentialgleichungssystemen für die abstrakte Abbildung der betrachteten Probleme modelliert. Transportzeiten werden durch die Verwendung von „Time-delays“ berücksichtigt. Auf Basis dieser Modelle wurden Theoreme formuliert und bewiesen, die die Stabilität eines Netzwerkes garantieren, unter der Voraussetzung der Existenz von Lyapunov-Funktionen der einzelnen Teilsysteme und einer im Teilprojekt entwickelten „Small-gain“-Bedingung. Hierbei wurden die Stabilitätseigenschaften „Input-to-State-Stability“ (ISS), „Local ISS“ (LISS) sowie „Input-to-State-Dynamical-Stability“ (ISDS) verwendet und jeweils Lyapunov-Funktionen für die entsprechenden Gesamtnetzwerke konstruiert. Zusätzlich sind damit quantitative Aussagen über das Produktionsnetzwerk möglich. Die Ergebnisse fließen in ingenieurswissenschaftliche Simulationsmodelle ein, wobei Synergieeffekte wechselseitig genutzt werden. Beispielsweise wurde mithilfe dieses dualen Vorgehens ein Schema zur Identifizierung von Stabilitätsregionen entwickelt, das den Vorteil einer enormen Zeitersparnis bei der Identifizierung im Vergleich mit einem rein simulativen Vorgehen aufweist.Publikationen
- S. Dashkovskiy, M. Görges, L. Naujok.
Autonomous control methods in logistics - a mathematical perspective.
Applied Mathematical Modelling, 36(7):2947-2960, Elsevier, 2012. - S. Dashkovskiy, A. Mironchenko.
Local ISS of Reaction-Diffusion Systems.
18th IFAC World Congress, 28.08.-02.09.2011, Mailand, Italien.
Proceedings of the 18th IFAC World Congress, S. 11018-11023, 2011. - S. Dashkovskiy, A. Mironchenko, L. Naujok.
Autonomous and Central Control of Production Networks.
Autonomous Cooperation and Control in Logistics, M. Hülsmann, B. Scholz-Reiter, K. Windt (Hrsg.), S. 27-43, Springer Verlag, 2011.DOI: 10.1007/978-3-642-19469-6_4
online unter: http://link.springer.com/chapter/10.1007%2F978-3-642-19469-6_4#page-2 - S. Dashkovskiy, M. Görges, L. Naujok.
Local input to state stability of production networks.
2nd International Conference on Dynamics in Logistics, 17.08.-21.08.2009, Bremen, Deutschland.
Proceedings of the 2nd International Conference on Dynamics in Logistics, S. 79-89, Springer Verlag, 2011.online unter: https://www.math.uni-bremen.de/zetem/cms/media.php/256/LDIC_Article_LISS_DashGoerNauj_FinalVersion.pdf
- S. Dashkovskiy, M. Görges, M. Kosmykov, A. Mironchenko, L. Naujok.
Modeling and stability analysis of autonomously controlled production networks.
Logistics Research, 3(2):145-157, Springer Verlag, 2011.DOI: 10.1007/s12159-011-0049-6
online unter: http://www.springerlink.com/content/12nm645q18k27673/ - S. Dashkovskiy, D. Efimov, E. Sontag.
Input to State Stability and Allied System Properties.
Automation and Remote Control, 72(8), 1579–1614, 2011. - S. Dashkovskiy, S. Pavlichkov.
Backstepping for nonsmooth MIMO nonlinear Volterra systems with noninvertible input-output maps and controllability of their large-scale interconnections.
Nonlinear Dynamics and Systems Theory, 11(4):411-424, 2011.online unter: http://sunrise-0014438.e-ndst.kiev.ua/v11n4/V11N4.pdf#page=79
- S. Dashkovskiy, L. Naujok.
ISDS small-gain theorem and construction of ISDS Lyapunov functions for interconnected systems.
Systems & Control Letters, 59(5):299-304, Elsevier, 2010.online unter: http://www.math.uni-bremen.de/zetem/cms/media.php/256/ISDSPaperCorrectedSubmittedtoJournal.pdf
- S. Dashkovskiy, L. Naujok.
Lyapunov-Razumikhin and Lyapunov-Krasovskii theorems for interconnected ISS time-delay systems.
19th International Symposium on Mathematical Theory of Networks and Systems (MTNS 2010), 05.07.-09.07.2010, Budapest, Ungarn.
Proceedings of the 19th International Symposium on Mathematical Theory of Networks and Systems, S. 1179-1184, 2010. - S. Dashkovskiy, H. Kreowski, S. Kuske, A. Mironchenko, L. Naujok, C. von Totth.
Production Networks as Communities of Autonomous Units and Their Stability.
International Electronic Journal of Pure and Applied Mathematics, 2(1):17-42, 2010. - B. Scholz-Reiter, M. Görges, T. Jagalski, L. Naujok.
Modelling and analysis of an autonomous control method based on bacterial chemotaxis.
43rd CIRP International Conference on Manufacturing Systems, 26.05.-28.05.2010, Wien, Österreich.
Proceedings of the 43rd CIRP International Conference on Manufacturing Systems, S. 699-706, Neuer Wissenschaftlicher Verlag, Wien, 2010. - S. Dashkovskiy, A. Mironchenko.
On the uniform input-to-state stability of reaction-diffusion systems.
49th IEEE Conference on Decision and Control, 15.12.-17.12.2010, Atlanta, USA.
Proceedings of the 49th IEEE Conference on Decision and Control, S. 6547-6552, 2010. - S. Dashkovskiy, H. Kreowski, S. Kuske, A. Mironchenko, L. Naujok, C. von Totth.
Production Networks as Communities of Autonomous Units and Their Stability.
3rd International Workshop on Graph Computation Models, 02.10.2010, Enschede, Niederlande.
Proceedings of the 3rd International Workshop on Graph Computation Models, S. 17-32, 2010. - S. Dashkovskiy, M. Kosmykov, A. Mironchenko, L. Naujok.
Application of the LISS Lyapunov-Krasovskii small-gain theorem to autonomously controlled production networks with time-delays.
Conference on Control and Fault-Tolerant Systems, 06.10.-08.10.2010, Nizza, Frankreich.
Proceedings of the Conference on Control and Fault-Tolerant Systems, S. 765-770, 2010. - S. Dashkovskiy, L. Naujok.
Quasi-ISS and Quasi-ISDS Reduced-Order Observers for interconnected Systems.
49th IEEE Conference on Decision and Control, 15.12.-17.12.2010, Atlanta, USA.
Proceedings of the 49th IEEE Conference on Decision and Control, S. 5732-5737, 2010. - S. Dashkovskiy, S. Pavlichkov.
Further Remarks on Global Stabilization of Generalized Triangular Systems.
19th International Symposium on Mathematical Theory of Networks and Systems (MTNS 2010), 05.07.-09.07.2010, Budapest, Ungarn.
Proceedings of the 19th International Symposium on Mathematical Theory of Networks and Systems, S. 1483-1487, 2010. - S. Dashkovskiy, S. Pavlichkov.
Adding an integrator and uniform ISS stabilization for switched MIMO triangular systems with unknown switched signal and right invertible input-output maps.
Kharkov University Vestnik , 931:99-112, 2010.online unter: http://vestnik-math.univer.kharkov.ua/Vestnik-KhNU-931-2010-pavlichkov.pdf
- S. Dashkovskiy, S. Pavlichkov.
Backstepping for nonsmooth MIMO nonlinear Volterra systems with noninvertible input-output maps.
8th IFAC Symposium on Nonlinear Control Systems, 01.09.-03.09.2010, Bologna, Italien.
Proceedings of the 8th IFAC Symposium on Nonlinear Control Systems, S. 1158-1162, 2010. - S. Dashkovskiy, N. A. Duffie.
Delay-Dependent Stability Analysis for Large Scale Production Networks of Autonomous Work Systems.
International Journal of Nonlinear Dynamics and Systems Theory, 10(1):55-63, 2010.online unter: http://www.math.uni-bremen.de/~dsn/Publications/2010-NDST-KaDaDu.pdf
- S. Dashkovskiy, M. Kosmykov, L. Naujok.
ISS of interconnected impulsive systems with and without time-delays.
8th IFAC Symposium on Nonlinear Control Systems, 01.09.-03.09.2010, Bologna, Italien.
Proceedings of the 8th IFAC Symposium on Nonlinear Control Systems, S. 831-836, 2010. - S. Dashkovskiy.
Exponential Synchronization of Master-Slave Neural Networks with Time-Delays.
European Control Conference 2009, 23.08.-26.08.2009, Budapest, Ungarn.
Proceedings of the European Control Conference 2009, S. 342-347, 2009.online unter: http://www.math.uni-bremen.de/~dsn/Publications/2009-ECC-KD-synchronization
- S. Dashkovskiy, L. Naujok.
Input-to-state dynamical stability of interconnected systems.
48th IEEE Conference on Decision and Control, 16.12.-18.12.2009, Shanghai, China.
Proceedings of the 48th IEEE Conference on Decision and Control, S. 1411-1416, 2009.online unter: https://www.math.uni-bremen.de/zetem/cms/media.php/210/ISDSsmallgainFinalSubmission.pdf
- N. A. Duffie, S. Dashkovskiy.
Local Capacity H∞ Control for Production Networks of Autonomous Work Systems with Time-Varying Delays.
European Control Conference 2009, 23.08.-26.08.2009, Budapest, Ungarn.
Proceedings of the European Control Conference 2009, S. 2378-2383, 2009.online unter: http://www.math.uni-bremen.de/~dsn/Publications/2009-ECC-KDD-delays
- S. Dashkovskiy, B. Rüffer, F. Wirth.
Applications of the general Lyapunov ISS small-gain theorem for networks.
47th IEEE Conference on Decision and Control, 12.12.-14.12.2008, Cancún, Mexiko.
Proceedings of the 47th IEEE Conference on Decision and Control, S. 25-30, 2008.online unter: http://www.math.uni-bremen.de/~dsn/Publications/2008-CDC-DRW-applications.pdf
- S. Dashkovskiy, B. Rüffer, F. Wirth.
Stability of autonomous vehicle formations using an ISS small-gain theorem for networks.
79th Annual Meeting of the International Association of Applied Mathematics and Mechanics, 31.03-04.04.2008, Bremen, Deutschland.
Proceedings in Applied Mathematics and Mechanics, 8(1):10911-10912, 2008.online unter: http://www.math.uni-bremen.de/~dsn/Publications/2008-PAMM-DRW-Formations.pdf
- S. Dashkovskiy, B. Rüffer, F. Wirth.
Stability of interconnections of ISS systems.
SICE 8th Annual Conference on Control Systems, 05.03.-07.03.2008, Kyoto, Japan.
Proceedings of the 8th Annual Conference on Control Systems, S. 52431-52434, 2008. - S. Dashkovskiy, B. Rüffer, F. Wirth.
A Lyapunov small-gain theorem for stronlgy connected networks.
7th IFAC Symposium on Nonlinear Control Systems, 22.08.-24.08.2007, Pretoria, Südafrika.
Proceedings of the 7th IFAC Symposium on Nonlinear Control Systems, S. 283-288, 2007.online unter: http://www.math.uni-bremen.de/~dsn/Publications/final-nolcos-iss-lyapunovfunctions.pdf
- S. Dashkovskiy, B. Rüffer, F. Wirth.
An ISS Small Gain Theorem for General Networks.
Mathematics of Control, Signals and Systems, 19(2):93-122, 2007.online unter: http://www.math.uni-bremen.de/~dsn/Publications/MCSS.pdf
- S. Dashkovskiy, B. Rüffer, F. Wirth.
Numerical Verification of local input-to-state stability for large networks.
46th IEEE Conference on Decision and Control, 12.12.-14.12.2007, New Orleans, USA.
Proceedings of the 46th IEEE Conference on Decision and Control, S. 4471-4476, 2007.online unter: http://www.math.uni-bremen.de/~dsn/Publications/2007-cdc-drw-numerical-liss-final.pdf
- B. Scholz-Reiter, F. Wirth, M. Freitag, S. Dashkovskiy, T. Jagalski, C. de Beer, B. Rüffer.
Some remarks on the stability of production networks. Stability margins.
Operations Research 2005, 07.09.-09.09.2005, Bremen, Deutschland.
Operations Research Proceedings 2005, S. 91-96, Springer Verlag, 2006.online unter: https://www.math.uni-bremen.de/zetem/cms/media.php/256/SFB637-A5-05-005-IC-1.pdf
- S. Dashkovskiy, B. Rüffer, F. Wirth.
An ISS Lyapunov Function for Networks of ISS Systems.
17th International Symposium on Mathematical Theory of Networks and Systems (MTNS 2006), 24.07.-28.07.2006, Kyoto, Japan.
Proceedings of the 17th International Symposium on Mathematical Theory of Networks and Systems, S. 77-82, 2006.online unter: http://www.math.uni-bremen.de/~dsn/Publications/MTNS-Lyapunov.pdf
- S. Dashkovskiy, F. Wirth, T. Jagalski.
Autonomous control in Shop Floor Logistics: Analytic models.
IFAC Conference on Manufacturing, Modelling, Management and Control, 21.10.-22.10.2004, Athen, Griechenland.
Manufacturing, Modelling, Management and Control 2004, G. Chryssolouris , D. Mourtzis (Hrsg.), Elsevier, 2006.online unter: http://www.math.uni-bremen.de/~dsn/Publications/ifac_Athen3.pdf
- S. Dashkovskiy, B. Rüffer, F. Wirth.
Discrete time monotone systems: Criteria for global asymptotic stability and applications.
17th International Symposium on Mathematical Theory of Networks and Systems (MTNS 2006), 24.07.-28.07.2006, Kyoto, Japan.
Proceedings of the 17th International Symposium on Mathematical Theory of Networks and Systems, S. 89-97, 2006.online unter: http://www.math.uni-bremen.de/~dsn/Publications/MTNS-Monotone.pdf
- S. Dashkovskiy, B. Rüffer, F. Wirth.
A Small-Gain type stability criterion for large scale networks of ISS systems.
44th IEEE Conference on Decision and Control and European Control Conference ECC 2005, 12.12.-15.12.2005, Sevilla, Spanien.
Proceedings of the 44th IEEE Conference on Decision and Control and European Control Conference ECC 2005, S. 5633-5638, 2005.online unter: http://www.math.uni-bremen.de/~dsn/Publications/CDCECC05.pdf
- S. Dashkovskiy, M. Kosmykov.
Stability analysis of logistics networks with time-delays.
Erscheint in Production Planning & ControlDOI: 10.1080/09537287.2012.659867
online unter: http://www.tandfonline.com/doi/abs/10.1080/09537287.2012.659867

