
Archimedische Körper

Catalanische Körper
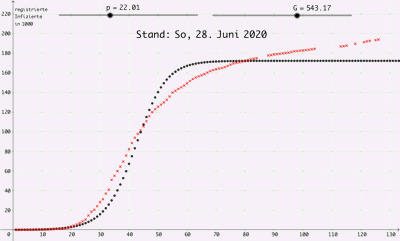
Logistisches Wachstum
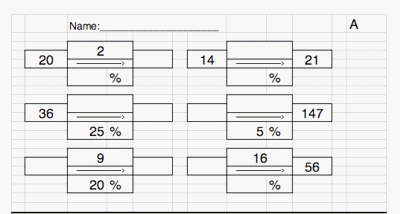
Test Grundfertigkeiten
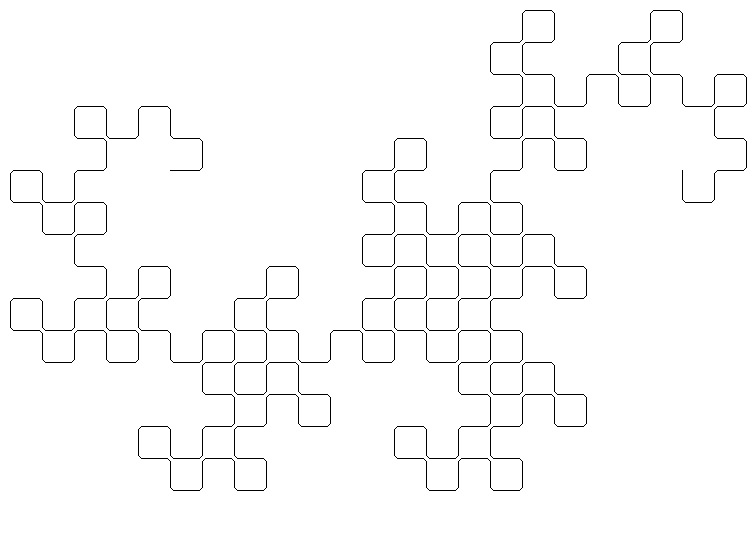
Papierfaltungs-Folge und Heighway-dragon
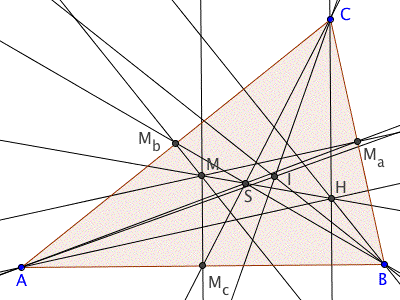
Dreieckszentren

Material von Vorträgen

| Platonische Körper |  Archimedische Körper |
 Catalanische Körper |
 Logistisches Wachstum |
 Test Grundfertigkeiten |
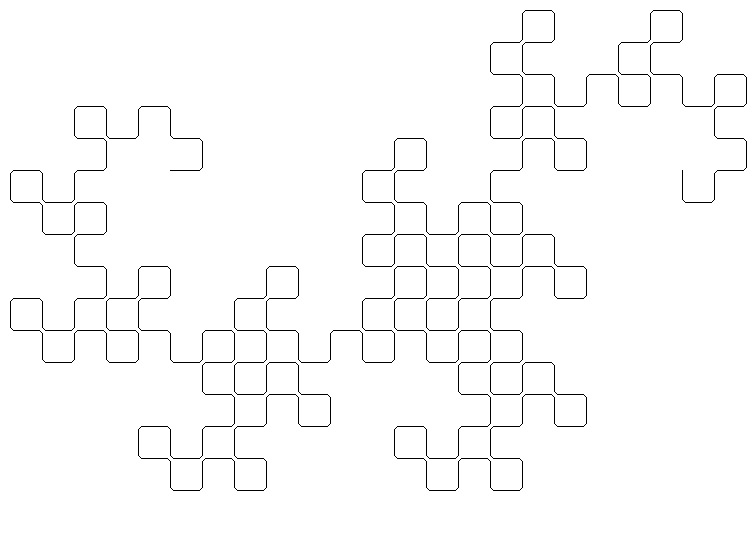 Papierfaltungs-Folge und Heighway-dragon |
 Dreieckszentren |
 Material von Vorträgen |
 |