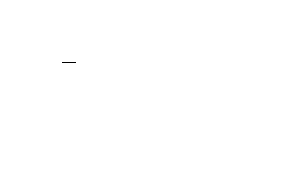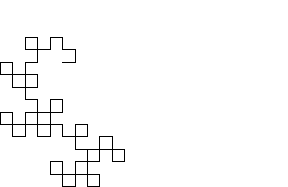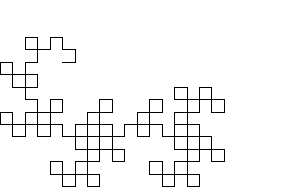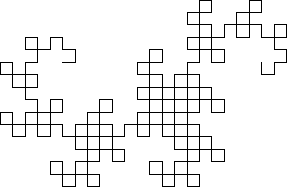
Legt man beim Auffalten Wert auf regelmäßige Winkel, in der Regel 90°, erhält man zusätzlich noch ein hochkomplexes geometrisches Muster, genannt den Heighway-Dragon, das Anlass gibt zu geometrischen Untersuchungen.
|
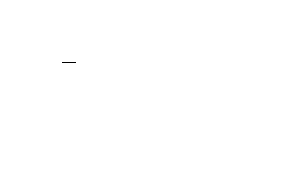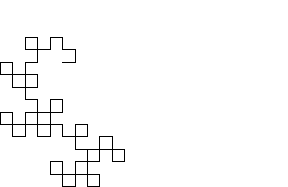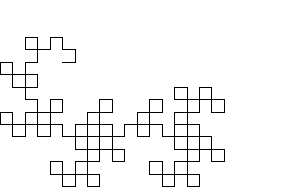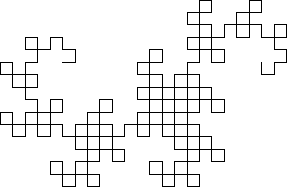Man nimmt einen Streifen
Papier und faltet ihn wiederholt auf die gleiche Weise in
der Mitte. Zieht man ihn auseinander, erhält man eine
Abfolge von Knicken, die Tal- oder Bergknicke sein können.
Das Studium dieser Knickfolge, der Papierfaltungsfolge,
bietet eine Fülle von Gesetzmäßigkeiten und mathematischen
Betrachtungen. Legt man beim Auffalten Wert auf regelmäßige Winkel, in der Regel 90°, erhält man zusätzlich noch ein hochkomplexes geometrisches Muster, genannt den Heighway-Dragon, das Anlass gibt zu geometrischen Untersuchungen. |
| Link |
Erläuterung |
| http://nbn-resolving.de/urn:nbn:de:gbv:46-diss000105747 | Der offizielle Link zu
meiner Dissertation über die Papierfaltungsfolge und den
Heighway-Dragon. |
| http://www.math.uni-bremen.de/didaktik/ma/ralbers/Materialien/Papierfalten/Dissertation/index.html |
Eine Informationsseite zu meiner Dissertation über die Papierfaltungsfolge |
| https://oeis.org/A014577 | This is the entrance of the paper-folding sequence in the on-line encyclopedia of interger sequences |
| http://cs.unm.edu/~joel/PaperFoldingFractal/paper.html | Some interesting information
and the software "fractal grower" (Java) |
| http://www.jgiesen.de/Divers/PapierFalten/PapierFalten.html | Eine Seite zu einer schulorientierten Einführung in die Papierfaltungsfolge mit vielen weitern Links |
| https://angelxuanchang.github.io/pubs/dragonbound.pdf |
A paper on the boundary of
the Highway-dragon |
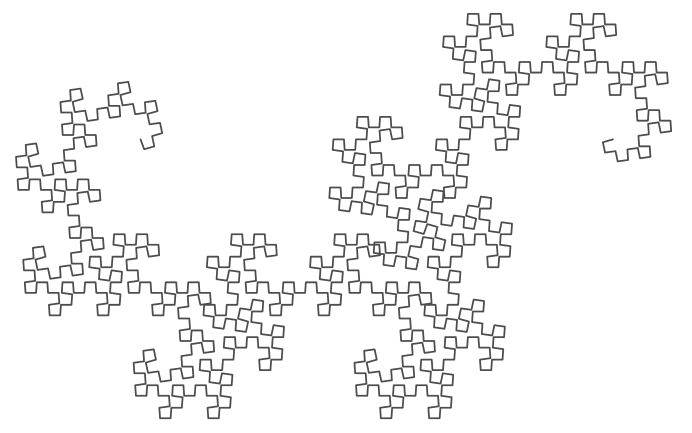Variiert man
den Auffaltungswinkel und wählt einen etwas größeren Winkel als 90°,
so ist die intuitive Annahme, dass dann die einzelnen
Streckenabschnitte einen Linienzug bilden, der keine doppelten
Punkte (Überschneidungen) aufweist. Diese Annahme ist bis zur 9.
Iteration richtig, ab der 10. Iteration treten für Auffaltwinkel
zwischen 90° und 95° Überschneidungen auf (siehe Abbildung links,
10. Iteration, Auffaltwinkel 94°).