Spektrale Wertemengen für struktutrierte Matrixstörungen
| Leitung: |
Prof. Dr. Diederich Hinrichsen (E-Mail: dh@math.uni-bremen.de)
|
| Bearbeitung: |
|
| Projektförderung: |
DFG Graduiertenkolleg Komplexe Dynamische Systeme |
| Projektpartner: |
Prof. Dr. Anthony J. Pritchard, University of Warwick, Großbritannien
|
| Laufzeit: |
01.05.1997 - 31.07.2003 |
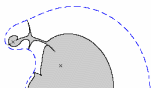
Die spektrale Wertemenge einer Matrix ist die Menge aller komplexen
Zahlen, in die wenigstens ein Eigenwert der Matrix durch Störungen
vorgegebener Struktur und Normschranke verschoben werden kann.
Spektrale Wertemengen haben sich in den letzten Jahren zu einem Werkzeug
entwickelt, das in zahlreichen Fragen der Unsicherheit und des
Übergangsverhaltens dynamischer Systeme und zur Untersuchung von
Verfahren der numerischen linearen Algebra angewandt wird.
Ziel des Projekts ist es, einen Beitrag zur Entwicklung der Theorie
spektraler Wertemengen zu leisten. Dabei sollen insbesondere reelle
Matrixstörungen untersucht werden, die bisher in der Literatur kaum
analysiert wurden. Die Hauptergebnisse des Projekts, die in die
Dissertation von Michael Karow einfließen, sind die folgenden:
- Spektrale Wertemengen hängen stetig von sämtlichen Parametern ab,
die in ihre Definition eingehen.
- Wenn die zugrunde liegende Norm und die zugrunde liegende
Störungsstruktur semialgebraisch sind, dann sind auch die zugehörigen
spektralen Wertemengen semialgebraisch. Ihr Rand ist daher stückweise
analytisch.
- Das asymptotische Verhalten spektraler Wertemengen für kleine
Störungen wird analysiert. Dabei werden Formeln für die Höldersche
Konditionszahl eines mehrfachen Eigenwerts unter strukturierten Störungen
angegeben. Diese Formeln verallgemeinern Resultate von Chatelin und
Harabi.
- Spektrale Wertemengen blockdiagonaler Matrizen werden diskutiert.
Diese sind relevant für das Stabilitätsverhalten gekoppelter linearer
Systeme. Es werden Formeln für die Berechnung der zugehörigen
mu-Funktionen hergeleitet. Dabei ergibt sich eine Verallgemeinerung
der klassischen Eigenwert-einschlusssätze von Gerschgorin, Brauer
und Brualdi.
- Der Zusammenhang der Größe der Pseudospektren einer Matrix mit deren
Nichtnormalität wird untersucht. Insbesondere wird der
Eigenwerteinschlusssatz von Henrici geeignet umformuliert und dann
für Blockdreiecksmatrizen verallgemeinert.
- Es wird gezeigt, dass die Menge der Unstetigkeitsstellen der reellen
mu-Funktion in der Menge der reellen Matrizen enthalten ist.
- Für die Berechnung reeller spektraler Wertemengen von normalen
Matrizen werden explizite Formeln angegeben. Somit wird ein von
Hinrichsen und Pritchard aufgeworfenes Problem gelöst.
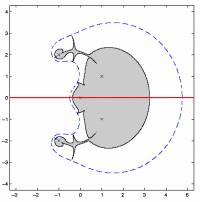
Das Bild zeigt die strukturierte reelle spektrale Wertemenge einer Diagonalmatrix A. Die Kreuze markieren die Eigenwerte von A. Die gestrichelte Kurve ist der Rand der analog definierten komplexen spektralen Wertemenge.
 Die spektrale Wertemenge einer Matrix ist die Menge aller komplexen
Zahlen, in die wenigstens ein Eigenwert der Matrix durch Störungen
vorgegebener Struktur und Normschranke verschoben werden kann.
Spektrale Wertemengen haben sich in den letzten Jahren zu einem Werkzeug
entwickelt, das in zahlreichen Fragen der Unsicherheit und des
Übergangsverhaltens dynamischer Systeme und zur Untersuchung von
Verfahren der numerischen linearen Algebra angewandt wird.
Ziel des Projekts ist es, einen Beitrag zur Entwicklung der Theorie
spektraler Wertemengen zu leisten. Dabei sollen insbesondere reelle
Matrixstörungen untersucht werden, die bisher in der Literatur kaum
analysiert wurden. Die Hauptergebnisse des Projekts, die in die
Dissertation von Michael Karow einfließen, sind die folgenden:
Die spektrale Wertemenge einer Matrix ist die Menge aller komplexen
Zahlen, in die wenigstens ein Eigenwert der Matrix durch Störungen
vorgegebener Struktur und Normschranke verschoben werden kann.
Spektrale Wertemengen haben sich in den letzten Jahren zu einem Werkzeug
entwickelt, das in zahlreichen Fragen der Unsicherheit und des
Übergangsverhaltens dynamischer Systeme und zur Untersuchung von
Verfahren der numerischen linearen Algebra angewandt wird.
Ziel des Projekts ist es, einen Beitrag zur Entwicklung der Theorie
spektraler Wertemengen zu leisten. Dabei sollen insbesondere reelle
Matrixstörungen untersucht werden, die bisher in der Literatur kaum
analysiert wurden. Die Hauptergebnisse des Projekts, die in die
Dissertation von Michael Karow einfließen, sind die folgenden:


