Ein effizientes Simulationsverfahren für Unterwasserschallwellen
| Arbeitsgruppe: | Ehemalige AG Inverse Probleme |
| Leitung: | Prof. Dr. Armin Lechleiter |
| Bearbeitung: | Dr. Tobias Rienmüller |
| Projektförderung: | Zentrale Forschungsförderung der Universität Bremen |
| Projektpartner: | |
| Laufzeit: | 01.11.2012 - 31.10.2015 |
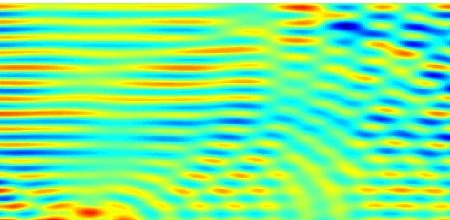 Die Berechnung der Ausbreitung von Unterwasserschall ist ein wichtiges Werkzeug der physikalischen und bioakustischen Meeresforschung mit zahlreichen konkreten Anwendungen. Traditionelle Simulationstechniken sind oft nicht präzise genug, um quantitative Aussagen mit hinreichender Fehlertoleranz treffen zu können. In großen Rechengebieten haben die üblichen akkuraten Simulationen, z.B. mit finiten Elementen, jedoch einen zu großen Rechen- und Speicheraufwand. Um diese Problematik zu umgehen beschreibt das hier untersuchte Verfahren die Schallwelle im Frequenzbereich durch eine Volumenintegralgleichung. Die spektrale Galerkin-Diskretisierung solcher Gleichungen hat den Vorteil, dass die Welle nur dort lokal simuliert werden muss, wo sie auf ein Hindernis trifft, aber nicht im Raum zwischen Hindernissen. Ziel des Projektes ist die Entwicklung und Analyse einer neuen Integralgleichungsmethode, die als effizientes Simulationswerkzeug für Unterwasserschall in realistischen Szenarien (geschichtete Strukturen, Schallgradienten) verwendet werden kann.
Die Berechnung der Ausbreitung von Unterwasserschall ist ein wichtiges Werkzeug der physikalischen und bioakustischen Meeresforschung mit zahlreichen konkreten Anwendungen. Traditionelle Simulationstechniken sind oft nicht präzise genug, um quantitative Aussagen mit hinreichender Fehlertoleranz treffen zu können. In großen Rechengebieten haben die üblichen akkuraten Simulationen, z.B. mit finiten Elementen, jedoch einen zu großen Rechen- und Speicheraufwand. Um diese Problematik zu umgehen beschreibt das hier untersuchte Verfahren die Schallwelle im Frequenzbereich durch eine Volumenintegralgleichung. Die spektrale Galerkin-Diskretisierung solcher Gleichungen hat den Vorteil, dass die Welle nur dort lokal simuliert werden muss, wo sie auf ein Hindernis trifft, aber nicht im Raum zwischen Hindernissen. Ziel des Projektes ist die Entwicklung und Analyse einer neuen Integralgleichungsmethode, die als effizientes Simulationswerkzeug für Unterwasserschall in realistischen Szenarien (geschichtete Strukturen, Schallgradienten) verwendet werden kann.
Publikationen
- A. Lechleiter, T. Rienmüller.
Collocation discretization for an integral equation in ocean acoustics with depth-dependent speed of sound.
Mathematical Methods in the Applied Sciences, 40(5):1608-1624, Wiley, 2017.DOI: 10.1002/mma.4082
- P. Monk, A. Lechleiter.
The Time Domain Lippmann-Schwinger Equation and Convolution Quadrature.
Numerical Methods for Partial Differential Equations, 31(2):517-540, Wiley, 2015.DOI: 10.1002/num.21921
online unter: Link (arXiv) - A. Lechleiter, T. Rienmüller.
Time-Harmonic Acoustic Wave Scattering in an Ocean with Depth-Dependent Sound Speed.
Applicable Analysis - An International Journal, 95:978-999, 2015. - T. Rienmüller.
Integral Equation Methods for Ocean Acoustics with Depth-Dependent Background Sound Speed.
Dissertationsschrift, Universität Bremen, 2015.online unter: http://nbn-resolving.de/urn:nbn:de:gbv:46-00104767-18

