DFG-SPP 1114: Wavelet-shrinkage in der Bildverarbeitung – Eine Untersuchung von Zusammenhängen und Äquivalenzen
| Arbeitsgruppe: | AG Technomathematik |
| Leitung: | Prof. Dr. Dr. h.c. Peter Maaß ((0421) 218-63801, E-Mail: pmaass@math.uni-bremen.de ) |
| Bearbeitung: | Prof. Dr. Dirk Lorenz ((0421) 218-63982, E-Mail: d.lorenz@uni-bremen.de ) |
| Projektförderung: | DFG (Schwerpunktprogramm 1114) |
| Projektpartner: | |
| Laufzeit: | 01.10.2002 - 30.09.2004 |

Zwei der wichtigsten Grundprobleme in der Bild- und Signalverarbeitung sind das Entrauschen von Daten und das Scharfzeichnen. Die dabei benutzten Methoden kommen aus den verschiedensten Bereichen der Mathematik: Statistik, Funktionalanalysis, Variationsrechnung, Wavelet-Theorie und harmonische Analysis sind nur einige. Viele dieser Methoden hängen eng zusammen und manche sind einfach dieselben in einer anderen Sprache formuliert. Die Untersuchung der Zusammenhänge der verschiedenen Methoden ist seit einigen Jahren Gebiet interessanter Forschungen.

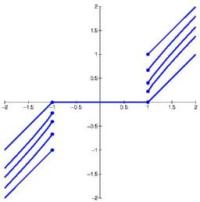
Eine mittlerweile sehr weit verbreitete Methode zum Entrauschen ist das Wavelet-Shrinkage. Bei dieser Methode werden Bilder in bestimmte Wavelet-Basen entwickelt und die Koeffizienten bezüglich dieser Basis mit einer nichtlinearen Funktion abgeändert. Das Wavelet-Shrinkage ist einerseits aufgrund seiner Einfachheit weit verbreitet, andererseits auch, weil es in vielen theoretischen Ansätzen sozusagen "von selbst" auftaucht. In der Dissertation von Dirk Lorenz werden die verschiedenen Zugänge, die zum Wavelet- Shrinkage führen, analysiert und ausgearbeitet. Darunter fallen Zugänge aus dem Bereich der Variationsrechnung, der Abstiegsgleichungen, der Theorie der Funktionenräume und auch der Statistik. Über die Einordnung bekannter Ergebnisse in einem gemeinsamen Rahmen hinaus werden in der Dissertation weitere, neue Zusammenhänge, insbesondere zu allgemeineren Shrinkage- Funktionen, beschrieben. Unter anderem wurden dabei neue Shrinkage-Funktionen entwickelt, die zwischen den Extremfällen des Soft- und des Hard-Shrinkage auf natürliche Weise interpolieren.