DFG-SPP 1114: Optimal musterangepasste Wavelets
| Arbeitsgruppe: | AG Technomathematik |
| Leitung: | Prof. Dr. Dr. h.c. Peter Maaß ((0421) 218-63801, E-Mail: pmaass@math.uni-bremen.de ) |
| Bearbeitung: | Dr. Henning Thielemann |
| Projektförderung: | DFG (Schwerpunktprogramm 1114) |
| Projektpartner: | Prof. Dr. Bernd Kuhfuß, WZM |
| Laufzeit: | seit 01.11.2001 |

Viele Anwendungen der Prozessüberwachung und Messdatenauswertung erfordern das Aufspüren eines Musters in einem Signal, wobei die Skalierung des Musters vorher nicht bekannt ist. Bei anderen Anwendungen wie der Datenkompression muss man eine Messreihe in diese Muster und einen nicht klassifizierbaren Rest zerlegen. Einige typische Beispiele aus Industrieprojekten des Zentrums für Technomathematik:
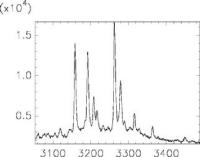
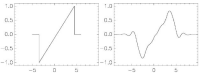
- Ein Massenspektrogramm besteht aus Spitzen, wobei jede Spitze ein bestimmtes Verhältnis von Teilchenmasse zu Ladung repräsentiert. Jede Spitze besitzt eine charakteristische Form (z.B. links ein steiler Anstieg, rechts ein etwas flacherer Abfall) und die Fläche unter der Kurve gibt an, wie häufig Teilchen mit einem bestimmten Masse- Ladungsverhältnis auf den Detektor getroffen sind. Da eine Art Teilchen unterschiedlich stark geladen sein kann, treten Spitzen für den gleichen Stoff an verschiedenen Stellen mit unterschiedlichen Breiten auf.
- Der Verschleiß in Kugellagern erzeugt charakteristische Abweichungen von einem ansonsten periodischen und mit Rauschen überlagerten Signal. Die Ausdehnung der Abweichungsmuster hängt dabei von der Rotationsgeschwindigkeit des Kugellagers ab.
- Die Dicke eines von einer Rotorspinnmaschine erzeugten Fadens kann von der Normdicke abweichen, wenn der Rotor verschmutzt ist. Die Form der Abweichung lässt Rückschlüsse auf die Art der Verschmutzung zu, aber die Ausdehnung des Musters im Signal hängt von der Abzugsgeschwindigkeit des Fadens ab.
Mit der kontinuierlichen Wavelet-Transformation kann man alle diese Probleme angehen, erhält aber eine kaum zu bewältigende Datenmenge. Die Frage ist also, wie man die Daten mit geringerem Speicherverbrauch und daher auch höherer Geschwindigkeit verarbeiten kann. Als effiziente Alternative hat sich die diskrete Wavelet-Transformation etabliert. In ihrer Grundform zerlegt sie ein Signal ohne Redundanz in mehrere verschobene und skalierte Versionen eines Grundmusters (Wavelet). Diskrete Standard-Wavelets ähneln aber in der Regel nicht den Mustern, wie sie in den Anwendungen auftreten. Tatsächlich kann man mithilfe des Lifting-Prinzips den Entwurf eines musterangepassten Wavelets auf ein lineares Ausgleichsproblem zurückführen. Die Glattheit des Analyse- Wavelets kann dabei beliebig hoch gewählt werden.
Bei der Anwendung der Wavelets zur Kompression benötigt man eine numerisch gutartige Rekonstruktion der Wavelet-Transformierten. Dafür ist eine gewisse Glattheit der Synthese- Wavelets Voraussetzung. Diese neigen aber zu einer fraktalen Struktur, die auf der Struktur verfeinerbarer Funktionen beruht. Man kann sich eine verfeinerbare Funktion vorstellen als die Faltung eines B-Splines mit einer rein fraktalen, verallgemeinerten Funktion (Distribution). Daraus ergeben sich zwei Ansatzpunkte für die Glättung musterangepasster Wavelets:
- Reduktion der Rauheit des fraktalen Anteils. Es hat sich gezeigt, dass sich eine akzeptable Glättung über diesen Parameter erst erreichen lässt, wenn das Wavelet kaum noch das Muster annähert.
- Erhöhung der Ordnung des B-Splines, ohne die Anzahl verschwindender Momente des Analyse-Wavelets zu erhöhen. Hierfür wurde eine modifizierte Wavelet-Transformation entwickelt.