DFG-SPP 1114: Optimal Pattern-Matched Wavelets
| Working Group: | WG Industrial Mathematics |
| Leadership: | Prof. Dr. Dr. h.c. Peter Maaß ((0421) 218-63801, E-Mail: pmaass@math.uni-bremen.de ) |
| Processor: | Dr. Henning Thielemann |
| Funding: | DFG (Schwerpunktprogramm 1114) |
| Project partner: | Prof. Dr. Bernd Kuhfuß, WZM |
| Time period: | since 01.11.2001 |

Many applications of process monitoring and measurement data evaluation require the tracing of a pattern in a signal, the scale of the pattern being unknown at the outset. Other applications such as data compression require that a series of measurements be decomposed into these patterns and a non-classifiable remainder. A few typical examples from industrial projects at the Centre for Industrial Mathematics:
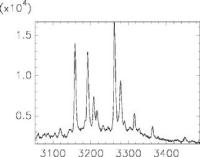
- A mass spectrogram consists of peaks, each peak representing a specific ratio of particle mass to charge. Each peak has a characteristic form (e.g. left a steep upward slope, right a somewhat flatter downwards slope) and the area underneath the curve gives the frequency with which particles with a certain mass-to-charge ratio have struck the detector. Since one species of particle can have different charge states, peaks occur for the same material at different locations with different widths.
- The wear and tear in ball-bearings produces characteristic deviations from an otherwise periodic signal on which noise is superimposed. The spread of the deviation pattern here depends on the speed of rotation of the ball-bearing.
- The thickness of a thread produced by a rotor-type open-end spinning machine can deviate from the standard thickness if the rotor is dirty. The form of the deviation allows one to draw conclusions about the type of dirt, but the spread of the pattern in the signal depends on the speed with which the thread is drawn off.
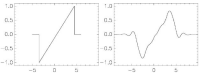
It is possible to tackle all these problems with continuous wavelet transformation but one obtains an almost insurmountable amount of data. The question, therefore, is how to process the data using a small amount of memory and hence also at higher speed. Discrete wavelet transformation has established itself as an efficient alternative. In its fundamental form it decomposes a signal without redundancy into several shifted and scaled versions of a fundamental pattern (wavelet). Discrete standard wavelets do not generally resemble the patterns as they occur in the applications, however. In reality, with the help of the lifting principle, it is possible to reduce the sketch of a pattern-matched wavelet to a linear fit problem. The smoothness of the analysis wavelet can be chosen so as to be arbitrarily high.
When using the wavelets for compression, a numerically benign reconstruction of the wavelet transform is required. The condition for this is a certain smoothness of the synthesis wavelets. These tend towards a fractal structure, however, which is based on the structure of refinable functions. A refinable function can be envisaged as the convolution of a B spline with a purely fractal, generalised function (distribution). This results in two starting points for the smoothing of pattern-matched wavelets:
- Reduction of the roughness of the fractal portion. It has turned out to be the case that an acceptable smoothing by means of this parameter can only be achieved when the wavelet hardly approximates to the pattern.
- Increasing the order of the B spline without increasing the number of vanishing moments of the analysis wavelet. A modified wavelet transformation has been developed for this.