Toleranzbasierte Regularisierungstheorie für inverse Probleme
| Arbeitsgruppe: | AG Technomathematik |
| Leitung: | Prof. Dr. Dr. h.c. Peter Maaß ((0421) 218-63801, E-Mail: pmaass@math.uni-bremen.de ) |
| Bearbeitung: |
Dr. Phil Gralla
Dr. Iwona Piotrowska-Kurczewski |
| Projektpartner: | LFM, Labor für Mikrozerspanung |
| Laufzeit: | seit 01.06.2015 |
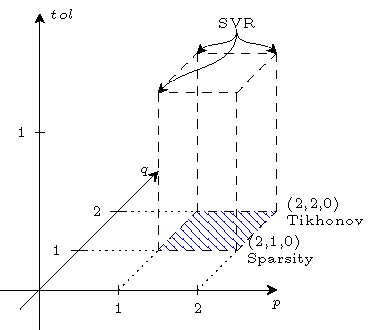
Tikhonov-Funktionale zum Lösen von inversen Problemen bestehen aus einem Diskrepanz- und einem Strafterm. Der Diskrepanzterm evaluiert die Diskrepanz zwischen modellierten und gemessenen Daten. Dieser Diskrepanzterm soll nun durch ein Toleranzmaß alterniert werden, um kleine Abweichungen der Daten innerhalb der vorgegebenen Toleranz zu ignorieren. Dieser Ansatz wird aus der Möglichkeit von Mehrfachmessungen in der Anwendung motiviert, wodurch ein Koinzidenzintervall für die exakte Messung angegeben wird. Dieser Ansatz ist bereits aus der Support Vector Regression (SVR) bekannt, bei der der betrachtete Operator die Identität ist.
Für Tikhonov-Funktionale der Form
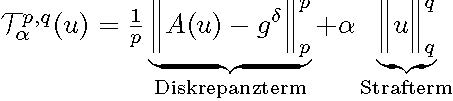
mit festem p und q ist die Regularisierungstheorie bereits gut untersucht. Die aktuelle Forschung am ZeTeM beschäftigt sich mit dem Bilden einer fundierten mathematischen Grundlage für Toleranzen im Diskrepanzterm von Tikhonov-Funktionalen für nichtlineare inverse Probleme. Erste Ergebnisse für Operatoren zwischen Hilbert- und Lebesgue-Räumen liegen vor und dienen als Grundlage für die weitere Forschung. Für die betrachteten Toleranzen wird eine epsilon-insensitive Distanzfunktion von Vapniak für SVR verwendet und die Definition erweitert, um eine Anwendung auf Elemente aus dem betrachteten Lebesgue-Räumen zu ermöglichen. In der nahen Zukunft werden die bisherigen Grundlagen für allgemeinere Räume erweitert und ein Algorithmus zum Lösen der inversen Probleme mit Toleranzen hergeleitet.
Durch die bestehende Kooperation mit dem Labor für Mikrozerspanung LFM und weiteren Partnern des Sonderforschungsbereichs 747 kann die erarbeitete Theorie an praktischen Beispielen getestet und angewendet werden. Bei der Mikrokaltumformung spielen Toleranzen eine entscheidende Rolle in der Qualität der produzierten Bauteile. Unsere Forschung liefert dabei einen wichtigen Beitrag zur Entwicklung neuer Methoden, die schneller und präziser Mikrobauteile durch Kaltumformung erzeugen. Dies wird vor allem in den Teilprojekten C2 und T4 des SFB 747, an denen das ZeTeM direkt beteiligt ist, ersichtlich.

