Parmeteridentifikation für reibungsbehaftete Signorini-Probleme
Ziel des Projekts ist die Entwicklung eines effizienten, adaptiven Algorithmus zur Parameteridentifikation bei reibungsbehafteten Signorini-Problemen. Eine besondere Herausforderung liegt dabei in der Tatsache, dass geometrische Kontaktbedingungen und Reibungsbedingungen zu einem nicht-glatten Parameter-zu-Zustands-Operator führen, der ableitungsbasierte Optimierungsmethoden nicht direkt anwendbar macht.

Zeitraum: 01.04.2023 - 30.09.2025
Leitung: Prof. Dr. Andreas Rademacher

Parameteridentifikation auf zeitabhängigen Gebieten mittels adaptiver Finite Zellen Methoden
Die Entwicklung eines adaptiven Algorithmus zur Parameteridentifikation auf zeitabhängigen Gebieten steht im Vordergrund des vorliegenden Projekts. Hierzu werden mittels eines parabolischen Modells Werte simuliert, deren Abstand zu gemessenen Referenzdaten minimiert werden soll. Die Zeitabhängigkeit wird dabei mit der Finite-Zellen-Methode berücksichtigt und die a posteriori Fehlerkontrolle verwendet dual gewichtete Residuen.

Zeitraum: 01.11.2022 - 31.10.2025
Leitung: Prof. Dr. Andreas Rademacher

Adaptive gemischte Finite Zellen Methoden für elliptische Probleme
Es ist eine große und aktuell noch unbefriedigend gelöste Herausforderung, den (reibungsbehafteten) Kontakt verschiedener Körper im Rahmen der Finite Zellen Methode (FCM) abzubilden. Das vorliegende Forschungsvorhaben geht einen ersten Schritt zur Bewältigung dieser Aufgabenstellung. Hier wird eine gemischte FCM entwickelt und analysiert, die fest vorgegebene Werte der Lösung auf dem fiktiven Rand abbilden kann. Dabei handelt es sich um eine wesentliche Teilaufgabe bei der Lösung von Kontaktproblemen.

Zeitraum: 01.04.2022 - 31.03.2025
Leitung: Prof. Dr. Andreas Rademacher, Prof. Dr. Lothar Banz

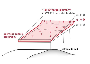Inverse Methoden zur Bestimmung von Höhenänderungen der Eisschildoberfläche mit einer Anwendung in der Westantarktis
Das vorliegende Forschungsprojekt befasst sich mit der Eisschildmodellierung des Westantarktischen Eisschildes (WAIS). Ziel ist die Entwicklung einer inversen Methode zur Optimierung der WAIS-Oberfläche unter Verwendung von Punktwolkendaten aus der Satellitenaltimetrie.

Zeitraum: 01.06.2021 - 31.05.2024
Leitung: Prof. Dr. Andreas Rademacher, Prof. Dr. Angelika Humbert

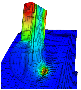Simulationsgestütztes NC-Formschleifen zur Endbearbeitung thermisch beschichteter Tiefziehwerkzeuge
Die Simulation von NC-Schleifverfahren steht im Vordergrund des vorliegenden Projekts, wobei geometrisch-kinematische und adaptive Finite-Elemente-Simulationen eingesetzt werden.

Zeitraum: 01.01.2015 - 15.06.2018
Leitung: Heribert Blum, Prof. Dr. Andreas Rademacher, Dirk Biermann, Prof. Dr.-Ing. Petra Wiederkehr geb. Kersting

Ort-Zeit-FEM für thermomechanisch gekoppelte Kontaktprobleme
Die Entwicklung von Ort-Zeit Finite Elemente Methoden steht im Vordergrund des vorliegenden Projektes. Dabei werden thermomechanisch gekoppelte Problemstellungen betrachtet und für die verschiedenen Größen unterschiedliche Netze eingesetzt.

Zeitraum: 01.07.2014 - 30.06.2015
Leitung: Prof. Dr. Andreas Rademacher

Adaptive Optimalsteuerung von Variationsungleichungen in der Mechanik
Variationsungleichungen finden sich bei der Modellierung von vielen verschiedenen physikalischen Vorgängen in der Mechanik. Hier steht die optimale Steuerung solcher Modelle auf Basis von adaptiven Finite Elemente Methoden im Vordergrund

Zeitraum: 15.07.2012 - 30.06.2015
Leitung: Prof. Dr. Andreas Rademacher, Prof. Dr. Christian Meyer

Entwicklung modelladaptiver Simulationsmethoden für umformtechnische Prozesse zur Herstellung komplexer Funktionsbauteile mit Nebenformen
Das vorliegende Projekt ist der Weiterentwicklung von modelladaptiven Algorithmen im Rahmen der Finite Elemente Methode gewidmet.

Zeitraum: 01.01.2012 - 31.12.2016
Leitung: Heribert Blum, Prof. Dr. Andreas Rademacher

Numerische Analyse und effiziente Implementierung komplexer FE-Modelle maschineller Fertigungsprozesse am Beispiel des Tiefbohrens
Die Simulation von maschinellen Fertigungsprozessen steht im Fokus dieses Forschungsprojekts. Zur Reduktion der Rechenzeit finden effizient parallelisierte adaptive Finite Elemente Methoden Anwendung.

Zeitraum: 01.05.2010 - 30.04.2017
Leitung: Heribert Blum, Prof. Dr. Andreas Rademacher, F.-T. Suttmeier