Parameter Identification for Signorini problems with friction
The aim of the project is to develop an efficient, adaptive algorithm for parameter identification in frictional Signorini problems. Gradient-based optimization methods are not easily applicable, as contact conditions and friction terms result in a non-smooth parameter-to-state operator. We thus smoothen the problem. A posteriori error analysis is used to balance different error influences.

Time period: 01.04.2023 - 30.09.2025
Leadership: Prof. Dr. Andreas Rademacher

Parameter Identification on Time-Dependent Domains using Adaptive Finite Cell Methods
The focus of the project at hand is the development of an adaptive algorithm for parameter identification on time-dependent domains. Therefore, a parabolic model is used to simulate values whose distance to measured reference data should be minimised. The time dependence is taken into account by means of the finite cell method and the a posteriori error control uses dual weighted residuals.

Time period: 01.11.2022 - 31.10.2025
Leadership: Prof. Dr. Andreas Rademacher

Adaptive mixed finite cell methods for elliptic problems
It is a major and currently still unsatisfactory challenge to map the (frictional) contact of different bodies using the finite cell method (FCM). The present research project takes a first step towards mastering this task. Here, a mixed FCM is developed and analyzed, which can map fixed values of the solution on the fictitious boundary. This is an essential subtask in the solution of contact problems.

Time period: 01.04.2022 - 31.03.2025
Leadership: Prof. Dr. Andreas Rademacher, Prof. Dr. Lothar Banz

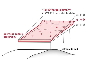Inverse methods for ice sheet surface elevation changes with an application to West Antarctica
The research project at hand focusses on ice sheet modeling of the West Antarctic Ice Sheet (WAIS). Here, we aim at developing a inverse method for optimizing the WAIS surface incorporating point cloud data from satellite altimetry.

Time period: 01.06.2021 - 31.05.2024
Leadership: Prof. Dr. Andreas Rademacher, Prof. Dr. Angelika Humbert

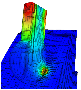Simulation-based NC-shape grinding as a finishing operation of coated deep drawing tools
The simulation of NC grinding processes is in the focus of the research project at hand. Here, geometric-kinematic as well as adaptive finite element simulations are used.

Time period: 01.01.2015 - 15.06.2018
Leadership: Heribert Blum, Prof. Dr. Andreas Rademacher, Dirk Biermann, Prof. Dr.-Ing. Petra Wiederkehr geb. Kersting

Space-time-FEM for thermomechanical coupled contact problems
The research project at hand is focused on the developement of space-time finite element methods. Here, we consider thermomechanical coupled problem setting, where the different quantities are discretized on different meshes.

Time period: 01.07.2014 - 30.06.2015
Leadership: Prof. Dr. Andreas Rademacher

Adaptive Optimal Control of Variational Inequalities in Computational Mechanics
The developement of adaptive finite element methods for the optimal control of variational inequalities is the main topic of the research project at hand.

Time period: 15.07.2012 - 30.06.2015
Leadership: Prof. Dr. Andreas Rademacher, Prof. Dr. Christian Meyer

Development of model adaptive simulation techniques for forming processes of complex functional components with complicated design details
The research project at hand aims at the developement of model adaptive algorithms inside of the finite element method.

Time period: 01.01.2012 - 31.12.2016
Leadership: Heribert Blum, Prof. Dr. Andreas Rademacher

Numerical analysis and efficient implementation of complex FE models of production processes based on the example of the deep hole drilling process
The simulation of production processes is in the focus of the research project at hand. We use efficiently parallelised adptive finite element methods to reduce the computing time.

Time period: 01.05.2010 - 30.04.2017
Leadership: Heribert Blum, Prof. Dr. Andreas Rademacher, F.-T. Suttmeier