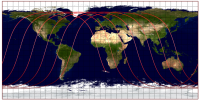
Optimierung von Satellitenüberdeckungen unter Berücksichtigung des ellipsoiden Erdmodells
| Arbeitsgruppe: | AG Optimierung und Optimale Steuerung |
| Leitung: | Prof. Dr. Christof Büskens ((0421) 218-63861, E-Mail: bueskens@math.uni-bremen.de ) |
| Bearbeitung: | Dr. Jan Vogelsang |
| Projektpartner: | |
| Laufzeit: | seit 01.04.2010 |
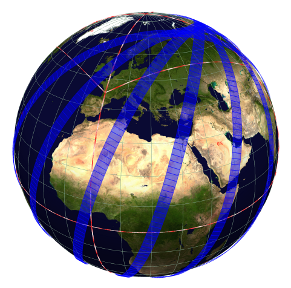
Bevor ein bestimmtes Gebiet auf der Erde mit orbitaler Sensorik beobachtet werden kann, müssen verschiedene Parameter, wie beispielsweise die Bahnelemente der Satellitenbahnen oder die Ein- und Ausschaltzeitpunkte der Sensoren, geeignet gewählt werden. Hierbei sollen diese Variablen unter Einhaltung verschiedener Restriktionen so gewählt werden, dass das von den Satelliten überstrichene Gebiet möglichst groß wird. Diese Optimierung lässt sich mit Verfahren aus der sequentiellen quadratischen Programmierung (SQP-Verfahren) durchführen.
Zur Anwendung dieser Verfahren wird jedoch eine differenzierbare Flächenrepräsentation der überdeckten Gebiete benötigt. In aktueller Software zur Analyse von Satellitenüberdeckungen wird jedoch meist ein diskretes Gitter verwendet. Dieses ist auf Grund der fehlenden Differenzierbarkeit nicht für SQP-Verfahren geeignet. Daher bieten sich Polygone als Flächenrepräsentation an. Je nach gewünschter Genauigkeit gibt es verschiedene Möglichkeiten zur Berechnung des polygonalen Flächeninhalts. Betrachtet man die Erde als Kugel, so führt dies zu sphärischen Polygonen, deren Fläche mit verschiedenen analytischen Methoden berechnet werden kann.
Eine bessere Annäherung an die reale Gestalt der Erde gelingt mit einem Rotationsellipsoiden. Die Flächeninhalte der geodätischen Polygone auf dem Ellipsoiden lassen sich durch Integrale beschreiben, die dann numerisch gelöst werden müssen. Die Kanten der Polygone werden durch geodätische Linien beschrieben, die den Großkreisen auf der Kugel entsprechen. Diese Probleme verlangen meist nach iterativen Verfahren, bei denen mit der sphärischen Repräsentation begonnen wird, die dann iterativ verbessert wird.
Die Beschränkung auf konvexe Polygone führt zu einigen Erleichterungen, z.B. bei der Untersuchung auf innere Punkte oder der Bestimmung von Polygonschnitten. Ist das von den Satellitensensoren beobachtete Gebiet durch konvexe geodätische Polygone dargestellt, so empfiehlt es sich, aus Effizienzgründen diese so weit wie möglich durch geeignete Vereinigungen zu vereinfachen. Hierdurch erhält man einen effizienten und hochgenauen Algorithmus zur Berechnung differenzierbarer Flächen auf einem Rotationsellipsoiden, der sich für die Optimierung mittels SQP-Verfahren eignet.
Nebenbedingungen, wie begrenzter Speicherplatz für die Sensordaten, Sonnenstand, Kontakt zu Bodenstationen, festgelegte Zeiten zwischen zwei Überdeckungen eines Gebiets, können bei der Optimierung berücksichtigt werden.