Effiziente Ableitungsberechnung über Graph Colouring
| Arbeitsgruppe: | AG Optimierung und Optimale Steuerung |
| Leitung: | Prof. Dr. Christof Büskens ((0421) 218-63861, E-Mail: bueskens@math.uni-bremen.de ) |
| Bearbeitung: | Dr. Patrik Kalmbach |
| Projektpartner: | |
| Laufzeit: | seit 01.09.2007 |
 Die meisten Lösungsverfahren von Optimierungsproblemen bestimmen so genannte Abstiegsrichtungen, durch welche man sukzessive ins Optimum eines Problems gelangt. Zur Bestimmung selbiger bedarf es der Berechnung oder Approximation von erster, häufig auch zweiter Ableitungen. Sofern diese nicht analytisch zur Verfügung stehen, sind numerische Berechnungen erforderlich.
Die meisten Lösungsverfahren von Optimierungsproblemen bestimmen so genannte Abstiegsrichtungen, durch welche man sukzessive ins Optimum eines Problems gelangt. Zur Bestimmung selbiger bedarf es der Berechnung oder Approximation von erster, häufig auch zweiter Ableitungen. Sofern diese nicht analytisch zur Verfügung stehen, sind numerische Berechnungen erforderlich.Die numerische Approximation über finite Differenzen wird dabei oft durch die Verwendung so genannter Update-Formeln vermieden, wodurch im Allgemeinen die Rechenzeit deutlich reduziert werden kann.
In dem von der Arbeitsgruppe Optimierung und Optimale Steuerung entwickelten Softwaretool WORHP werden keinerlei Updateformeln verwendet. Bei hochdimensionalen Problemen werden die Update-Techniken zu aufwändig, darüberhinaus können aufgrund der dünn besetzten Struktur der auftretenden Matrizen häufig zahlreiche Berechnungen eingespart werden, wodurch sich die „exakte Approximation“ durch die finiten Differenzen rentiert.
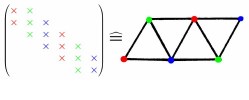
Nulleinträge in den auftretenden Matrizen brauchen nicht berechnet zu werden. Weiterhin können bei einer vektorwertigen Funktion mit einer dünn besetzten Jacobimatrix zahlreiche Spalten gleichzeitig berechnet werden. Die Zusammenfassung möglichst vieler Spalten zu möglichst wenigen Spalten-Gruppen führt auf ein äquivalentes Problem aus der Graphtheorie. Zwei Spalten dürfen zu einer Gruppe zusammengefasst werden, wenn es keine Zeile gibt, in der beide Spalten einen Eintrag haben. Ein Graph besteht aus einer Menge von Ecken und Kanten, wobei eine Kante eine Verbindungsstrecke zweier Ecken darstellt. Im Graph Colouring Problem soll die minimale Anzahl an zulässigen Farben gefunden werden, sodass alle Ecken eingefärbt werden, aber keine zwei Ecken, die miteinander verbunden sind, die gleiche Farbe besitzen. Man kann also die Spalten einer Matrix mit den Ecken eines Graphen identifizieren und zwei korrespondierende Ecken durch eine Kante verbinden, wenn sie in einer und derselben Zeile einen Eintrag aufweisen. In diesem Sinne sind daher Matrix und Graph verwandt.
Es ist bekannt, dass das Graph Colouring Problem NP-hard ist. Das heißt, mit steigender Dimension lässt sich die minimale Anzahl an Gruppen nicht in akzeptabler Zeit lösen. Daher bedarf es Alternativen, welche eine zulässige Colorierung liefern, die nah an die minimale Anzahl heranreicht und dennoch nur wenig Rechenzeit benötigt.
Das Konzept, Graph Colouring Algorithmen einzusetzen lässt sich auf Tensor-Ableitungen erweitern, wie sie innerhalb von WORHP benötigt werden.

