Simulation eingeschwungener und autonomer Systeme in Mikroelektronik und Mikrosystemtechnik
| Arbeitsgruppe: | Ehemalige AG Numerik |
| Leitung: | Prof. Dr. Angelika Bunse-Gerstner (E-Mail: bunse-gerstner@math.uni-bremen.de ) |
| Bearbeitung: | |
| Projektförderung: | FNK (Universität Bremen) |
| Projektpartner: | |
| Laufzeit: | 01.10.1998 - 31.07.2002 |

Die AG Numerik und das Institut für Theoretische Elektrotechnik
und Mikroelektronik (ITEM) der Universität Bremen führen seit
mehreren Jahren ein interdisziplinäres Projekt zur Entwicklung
von Simulationswerkzeugen für den Entwurf hochintegrierter
mikroelektronischer Schaltungen durch. Das Design derartiger
Schaltungen, die inzwischen in fast allen, auch den alltäglichsten,
technischen Geräten verwendet werden, ist ohne numerische Simulation
nicht durchzuführen. Die aktuell in der Industrie verwendeten
Simulationsalgorithmen können für bestimmte Schaltungen keine
oder keine befriedigenden Simulationsergebnisse liefern.
In diesem Projekt werden neue numerische Verfahren entwickelt,
die Lösungsstrategien für einige dieser Problemklassen zur
Verfügung stellen.
So verursacht zum Beispiel die Simulation von elektrischen
Schaltungen mit Elementen, die auf stark unterschiedlichen
Zeitskalen arbeiten (Mischer, Filter, Konverter, RF-Schaltungen, etc.)
große numerische Schwierigkeiten:
- Die Lösung enthält oft stark oszillierende Anteile unterschiedlicher Frequenzen.
- Die Integrationsschrittweite muss sich nach der kleinsten vorkommenden Zeitskala richten.
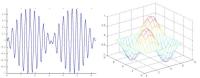
Diese Einbettung ermöglicht die Ausnutzung von Periodizitätsbedingungen,
so dass man sich zur Berechnung der mehrdimensionalen Funktionen auf
einen kleinen Periodizitätsbereich beschränken kann. Die Auswertung
der Funktion mehrerer Veränderlicher auf einem geeigneten Pfad liefert
die ursprüngliche Funktion zurück.
In den obigen Abbildungen wird dieser Vorgang veranschaulicht.
Um diesen Vorteil auszunutzen, ist ein Einbettungsverfahren entwickelt
worden, das die beschreibende gewöhnliche differentiell-algebraische
Gleichung eines Schaltkreises in eine partiell-algebraische
Differentialgleichung einbettet:
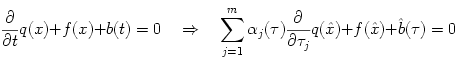
Hierbei ist x der gesuchte Vektor der Knotenspannungen und Zweigströme, q enthält Ladungs- und Flussterme, f stationäre Ströme und Spannungen und b die Eingangssignale. Die Funktion x^ ist die multivariable Einbettung von x, analog b^ von b, und a enthält den Weg der Auswertung. Die Berechnung der Lösung der partiellen Differentialgleichung auf dem Periodizitätsbereich ist unter gewissen Umständen wesentlich günstiger als die Lösung der differentiell-algebraischen Ausgangsgleichung. Dieser Übergang eröffnet neue Blickwinkel, die zur Entwicklung prinzipiell neuer Verfahren führen. Neben der theoretischen Untersuchung werden diese Verfahren implementiert und getestet. Aus diesem Forschungsbereich sind die Dissertation von Barbara Lang und die Diplomarbeit von Henning Lemanczyk entstanden. Weitere Themen dieses Projekts waren:
- Eine Schwierigkeit der Schaltkreissimulation besteht in der zuverlässigen Bestimmung von Grenzzyklen autonomer Schaltungen. Der Einzugsbereich konvergenter Startlösungen für praxisrelevante Schaltungen konnte quantitativ verbessert werden. Ein nächstes Ziel ist die Bestimmung sämtlicher stabiler und instabiler Grenzzyklen autonomer Systeme. Die Stabilitätsuntersuchung erfolgt dabei mittels Floquet-Theorie.
- Der algebraische Aspekt der Schaltkreisgleichungen wurde in bisherigen Simulationspaketen weitgehend ignoriert. Auch in der anwendungsbezogenen mathematischen Forschung werden differentiell-algebraische Gleichungen noch nicht sehr lange intensiv analysiert. Der Einfluss des algebraischen Anteils auf Simulationsergebnisse wird hier untersucht. Das Projekt leistet somit einen Beitrag, die Schaltungssimulation auf weitere Schaltungsklassen auszudehnen bzw. die Simulationsergebnisse auf eine qualitativ höhere Stufe zu stellen.