Fehlerabschätzungen und Adaptive Finite-Elemente-Methoden für Phasenfeldprobleme
| Arbeitsgruppe: | AG Numerik PDE |
| Leitung: | Prof. Dr. Alfred Schmidt ((0421) 218-63851, E-Mail: alfred.schmidt@uni-bremen.de ) |
| Bearbeitung: | |
| Projektpartner: |
Prof. Dr. Zhinin Chen, Beijing, China Prof. Dr. Ricardo H. Nochetto, University of Maryland, College Park, USA Daniel Kessler, University of Maryland, College Park, USA Prof. Dr. Claudio Verdi, Universität Mailand, Italien |
| Laufzeit: | seit 01.01.1998 |
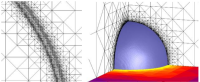
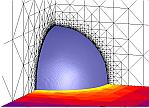 Bei der mathematischen Modellierung von Phasenübergängen treten einige der klassischen Beispiele für stark nichtlineare partielle Differentialgleichungen bzw. Systeme aus solchen Gleichungen auf. Diese Probleme sind daher nicht nur aus Sicht der Anwendungen von hohem Interesse, sondern auch aus rein mathematischer Perspektive. Durch Einführung der Phasengrenze als zusätzlichem Freiheitsgrad können auch Phasenübergänge modelliert werden, bei denen die Schmelztemperatur keine Materialkonstante ist, sondern wo die Temperatur des Phasenübergangs von lokalen Größen wie der Krümmung und der Geschwindigkeit der Phasengrenze abhängt. Bei einer klassischen Formulierung führt solch ein Gibbs-Thomson-Gesetz auf eine zusätzliche Bewegungsgleichung für die (glatte) Phasengrenzen-Hyperfläche. Durch Einführung einer zusätzlichen Phasenvariablen können auch solche Fälle modelliert werden, bei denen sich die Topologie der Phasengrenze ändert (z.B. durch Nukleation, Abschnüren oder Zusammenwachsen verschiedener Teile). Darüber hinaus bietet ein Phasenfeldmodell weitere Möglichkeiten für Modellierungen, die im Rahmen einer klassischen Formulierung nicht einfach geleistet werden können, und ist sogar auf einer physikalischen Mesoskala motivierbar.
Die mathematische Formulierung führt auf ein gekoppeltes System aus Diffusionsgleichungen für die Temperatur bzw. Konzentrationen sowie eine Allen-Cahn- oder Cahn-Hilliard- Gleichung für die Phasenvariable. Bei Verwendung eines Double-Obstacle-Potentials führt die entsprechende Allen-Cahn-Gleichung auf eine parabolische Variationsungleichung. In Zusammenarbeit mit Zhinin Chen und Ricardo Nochetto wurden Fehlerabschätzungen und adaptive Methoden für das Double-Obstacle-Phasenfeldmodell hergeleitet. Diese Betrachtung derartiger Probleme führte auch zur Entwicklung allgemeiner Multi-Mesh Finite-Elemente- Methoden zur Diskretisierung gekoppelter Systeme. Bei der Herleitung der Fehlerabschätzungen für das zeitabhängige Problem muss üblicherweise ein Gronwall-Argument benutzt werden, wodurch die Konstanten in exponentieller Weise vom Regularisierungsparameter abhängen. Durch Ausnutzung von speziellen Eigenwertabschätzungen von Xinfu Chen kann in Spezialfällen eine polynomiale Abhängigkeit erzielt werden; diese Abschätzungen werden in Zusammenarbeit mit Daniel Kessler und Ricardo Nochetto entwickelt. Besondere Bedeutung erhalten diese mathematischen Ergebnisse für die Zusammenarbeit im Sonderforschungsbereich 570, wo im Teilprojekt C4 mesoskopische Modelle für fest-fest Phasenumwandlungen mit Thermo-Elasto-Plastizität untersucht werden.
Bei der mathematischen Modellierung von Phasenübergängen treten einige der klassischen Beispiele für stark nichtlineare partielle Differentialgleichungen bzw. Systeme aus solchen Gleichungen auf. Diese Probleme sind daher nicht nur aus Sicht der Anwendungen von hohem Interesse, sondern auch aus rein mathematischer Perspektive. Durch Einführung der Phasengrenze als zusätzlichem Freiheitsgrad können auch Phasenübergänge modelliert werden, bei denen die Schmelztemperatur keine Materialkonstante ist, sondern wo die Temperatur des Phasenübergangs von lokalen Größen wie der Krümmung und der Geschwindigkeit der Phasengrenze abhängt. Bei einer klassischen Formulierung führt solch ein Gibbs-Thomson-Gesetz auf eine zusätzliche Bewegungsgleichung für die (glatte) Phasengrenzen-Hyperfläche. Durch Einführung einer zusätzlichen Phasenvariablen können auch solche Fälle modelliert werden, bei denen sich die Topologie der Phasengrenze ändert (z.B. durch Nukleation, Abschnüren oder Zusammenwachsen verschiedener Teile). Darüber hinaus bietet ein Phasenfeldmodell weitere Möglichkeiten für Modellierungen, die im Rahmen einer klassischen Formulierung nicht einfach geleistet werden können, und ist sogar auf einer physikalischen Mesoskala motivierbar.
Die mathematische Formulierung führt auf ein gekoppeltes System aus Diffusionsgleichungen für die Temperatur bzw. Konzentrationen sowie eine Allen-Cahn- oder Cahn-Hilliard- Gleichung für die Phasenvariable. Bei Verwendung eines Double-Obstacle-Potentials führt die entsprechende Allen-Cahn-Gleichung auf eine parabolische Variationsungleichung. In Zusammenarbeit mit Zhinin Chen und Ricardo Nochetto wurden Fehlerabschätzungen und adaptive Methoden für das Double-Obstacle-Phasenfeldmodell hergeleitet. Diese Betrachtung derartiger Probleme führte auch zur Entwicklung allgemeiner Multi-Mesh Finite-Elemente- Methoden zur Diskretisierung gekoppelter Systeme. Bei der Herleitung der Fehlerabschätzungen für das zeitabhängige Problem muss üblicherweise ein Gronwall-Argument benutzt werden, wodurch die Konstanten in exponentieller Weise vom Regularisierungsparameter abhängen. Durch Ausnutzung von speziellen Eigenwertabschätzungen von Xinfu Chen kann in Spezialfällen eine polynomiale Abhängigkeit erzielt werden; diese Abschätzungen werden in Zusammenarbeit mit Daniel Kessler und Ricardo Nochetto entwickelt. Besondere Bedeutung erhalten diese mathematischen Ergebnisse für die Zusammenarbeit im Sonderforschungsbereich 570, wo im Teilprojekt C4 mesoskopische Modelle für fest-fest Phasenumwandlungen mit Thermo-Elasto-Plastizität untersucht werden.