Nicht-negative Matrix-Faktorisierung mit A-priori-Wissen
| Arbeitsgruppe: | AG Technomathematik |
| Leitung: | Prof. Dr. Dr. h.c. Peter Maaß ((0421) 218-63801, E-Mail: pmaass@math.uni-bremen.de ) |
| Bearbeitung: |
Delf Lachmund
Dr. Pascal Fernsel ((0421) 218-63814, E-Mail: p.fernsel) Dr. Yovany Cordero Hernandez Dr. Tobias Boskamp |
| Projektpartner: | |
| Laufzeit: | seit 01.12.2014 |
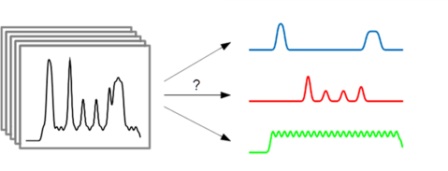
Schematische Darstellung der Blind Source Separation: Zu einer großen Menge von Mischsignalen werden die zugrunde liegenden Basismuster gesucht
Aufgrund neuer technologischer Möglichkeiten werden in verschiedensten Bereichen anfallende Datenmengen immer größer, sodass eine effiziente Verarbeitung der Daten ohne vorherige Dimensionsreduktion nicht mehr praktikabel ist. Typische Herangehensweisen beinhalten ein Thresholding der Daten in einer geeigneten Basisrepräsentation, z.B. einer Waveletbasis, oder eine unvollständige Singulärwertzerlegung. Das Ziel ist jeweils, bei größtmöglicher Datenreduktion nur unwichtige Informationen wegzuwerfen.
Eine spezielle Situation ergibt sich, wenn die Messdaten nicht beliebige Werte annehmen können, sondern nur innerhalb einer bestimmten Teilmenge gemessen werden. Dies ist z.B. der Fall, wenn aus physikalischen Gründen nur nicht-negative Datenwerte auftreten können. Ist zudem zu erwarten, dass die Messdaten bis auf Rauschen stets positive Linearkombinationen weniger unbekannter, nicht-negativer Basismuster sind, liegt ein typischer Fall von Blind Source Separation mit Positivitätsnebenbedingung vor.
Algorithmen zur nicht-negativen Matrix-Faktorisierung (NMF) versuchen nun, für einen solchen Datensatz beides gleichzeitig zu finden: eine Liste geeigneter Basismuster und die entsprechenden Koeffizienten der Linearkombinationen, jeweils mit der Einschränkung auf nicht-negative Werte. Im Falle bekannter Basismuster oder bekannter Linearkombinationen sind die zugehörigen Standardfunktionale konvex. Dies gilt jedoch nicht mehr, wenn beide unbekannt sind. Eine eindeutige Lösung kann daher nicht erwartet werden, und Näherungslösungen müssen iterativ ermittelt werden.
Hat man eine solche Näherungslösung gefunden, so liegt mit der Faktorisierung eine dimensionsreduzierte Repräsentation der Daten als Linearkombination weniger erlernter Basismuster vor. Unter gewissen Modellannahmen ist davon auszugehen, dass diese Muster starke Ähnlichkeit zu den unbekannten, eingangs postulierten Basismustern aufweisen.
Mithilfe dieser Muster können nun neue, den ursprünglichen Daten ähnliche Datensätze in besonderer Weise strukturiert werden. Es müssen hierzu lediglich die zu den erlernten Basismustern gehörenden Linearkoeffizienten bestimmt werden, was wesentlich einfacher zu realisieren ist. In Aufgabenstellungen des Machine Learnings bietet es sich somit an, solche Basismuster mitzulernen und die Koeffizienten beim Training statistischer Klassifikatoren zu berücksichtigen.
Zentrale Aufgabe in diesem Forschungsprojekt ist die Anpassung der NMF-Funktionale durch Hinzunahme verschiedener A-priori-Informationen, sowie die Entwicklung numerisch effizienter Algorithmen. Zu dem betrachteten A-priori-Wissen gehören einerseits Sparsity- und Orthogonalitätsforderungen und andererseits verfügbare Labelinformationen aus annotierten Trainingsdaten. Durch die Berücksichtigung der Labelinformationen wird diese Methode zu einer überwachten Merkmalsextraktion (Supervised Feature Extraction) und erlaubt idealerweise das Auffinden von feineren Basismustern, die von Standardalgorithmen als zu unwichtig erachtet und somit ignoriert werden.
Bei den in der Bioinformatik-Gruppe untersuchten MALDI-Imaging-Daten liegt das geschilderte Szenario vor. Die Basismuster können als spektrale Fingerprints interpretiert und die zugehörigen Koeffizienten in Form von Falschfarbenbildern visualisiert werden. Diese Anwendung liefert somit einen exzellenten Prüfstein für die neu entwickelten Verfahren.

