Sensitivitätsanalyse und Numerische Methoden bei großskalierten Systemen
| Arbeitsgruppe: | AG Optimierung und Optimale Steuerung |
| Leitung: |
Prof. Dr. Christof Büskens ((0421) 218-63861, E-Mail: bueskens@math.uni-bremen.de )
Dr.-Ing. Dennis Wassel |
| Bearbeitung: | Dr.-Ing. Sonja Rauki |
| Projektförderung: | The European Union under the 7th Framework Programme «FP7-PEOPLE-2010-ITN», Grant agreement number 264735-SADCO |
| Projektpartner: | Astos Solutions |
| Laufzeit: | seit 01.03.2011 |
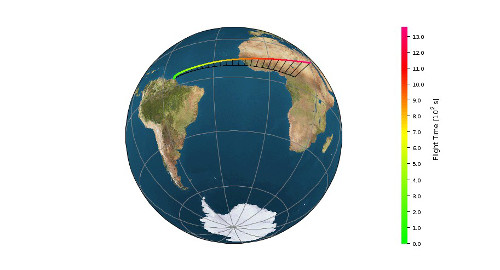
Nichtlineare Optimierung und Optimalsteuerung wird in der Luft- und Raumfahrtindustrie eingesetzt, andere industriell relevante Anwendungsbereiche sind der Energiesektor, chemische Reaktoren oder Verkehrssteuerung. Im Verbund „Sensitivity Analysis for Deterministic Controller Design – SADCO“, der von der Europäischen Kommission gefördert wird, haben sich deshalb acht akademische und drei industrielle Partner zusammengeschlossen, um dem Forschungs- und Entwicklungsbedarf in diesen Bereichen gerecht zu werden. Schwerpunkte sind dabei die Sensitivitätsanalyse sowie echtzeitfähige Regelungsalgorithmen. Aktuell befindet sich der SADCOVerbund in der Phase „Initial Training Network“, bei dem 17 Doktoranden aus ganz Europa die Gelegenheit zur Promotion haben.
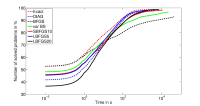
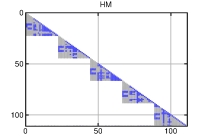
In der Luft- und Raumfahrtindustrie, insbesondere bei der Lösung von diskretisierten Problemen der optimalen Steuerung mit gewöhnlichen Differentialgleichungen, differential-algebraischen Gleichungen und partiellen Differentialgleichungen, entstehen Aufgaben, die in der Regel von hoher Dimension sind und eine dünnbesetzte Struktur aufweisen. Diese Struktur kann ausgenutzt werden, um performante und speichereffiziente Algorithmen zu entwickeln; dabei muss man möglichst viele Informationen des zugrunde liegenden Problems nutzen. Hierzu ist beispielsweise eine effiziente Anpassung der Hesse-Matrix der Lagrange-Funktion erforderlich.
Im Promotionsvorhaben von Sonja Rauški wurde untersucht, wie das Limited-BFGS-Verfahren bei hochdimensionalen, schwachbesetzten Problemen eingesetzt werden kann – so stellt diese Arbeit einen neuen Ansatz für hochdimensionale Optimierungsprobleme dar.