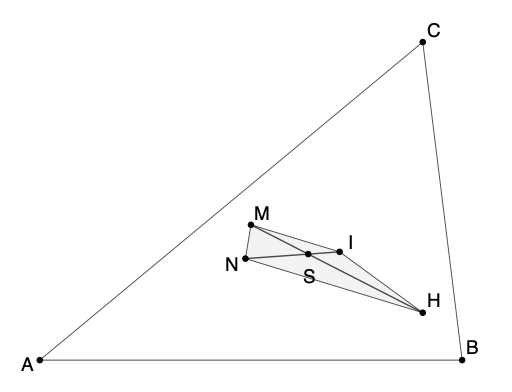
Die vier Zentren Nagel-Punkt N, Höhenschnittpunkt H, Inkreismittelpunkt I und Umkreismittelpunkt M bilden ein Trapez mit den parallelen Seiten NH und MI. Für deren Länge gilt |NH| = 2·|MI|. Die Diagonalen NI und MH schneiden sich im Schwerpunkt S.

Beweis
Wie gezeigt liegen H, S und M auf einer Geraden, der Euler-Geraden. Dabei teilt S die Strecke MH im Verhältnis 1:2 mit 2·|MS| = |SH|.
Wie ebenfalls gezeigt liegen N, S und I auf einer Geraden, der Nagel-Geraden. Dabei teilt S die Strecke NI im Verhältnis 1:2 mit 2·|SI| = |NS|.
Also ist der Schnittpunkt der beiden Geraden der Schwerpunkt S. Wegen des gleichen Teilverhältnisses gilt nach der Umkehrung des ersten Strahlensatzes (Strahlzentrum S), dass MI||NH ist. Über den zweiten Strahlensatz ermittelt man, dass MI halb so lang ist wie die Strecke NH.

R. Albers, erstellt mit GeoGebra