Satz

Der Nagelpunkt N liegt mit dem Schwerpunkt S und dem Inkreismittelpunkt I auf einer Geraden, der Nagel-Geraden. Dabei teilt der Schwerpunkt S die Strecke NI im Verhältnis 2:1, so dass gilt: |NS| = 2·|SI|.

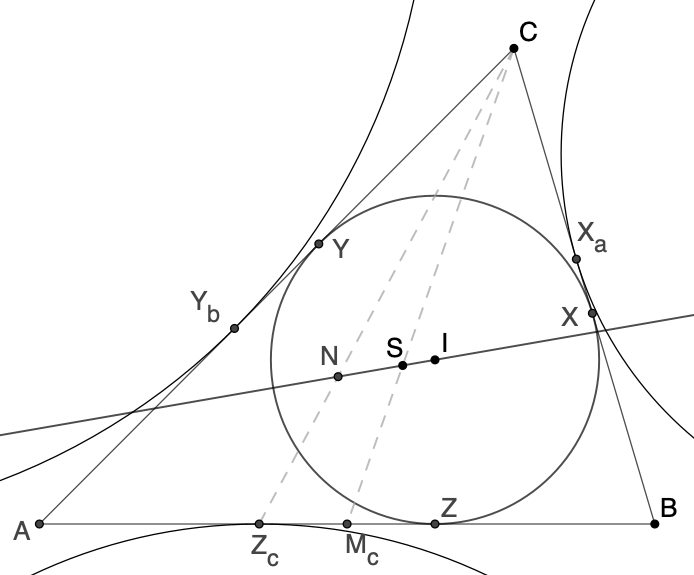
Beweis
(Auch diese Beweise folgen dem Original von Nagel)
Als Voraussetzung wird der Satz verwendet, dass die Ecktransversale durch den Nagelpunkt N parallel ist zur Geraden durch den Inkreismittelpunkt I und dem zugehörigen Seitenmittelpunkt (siehe hier).

Hilfssatz
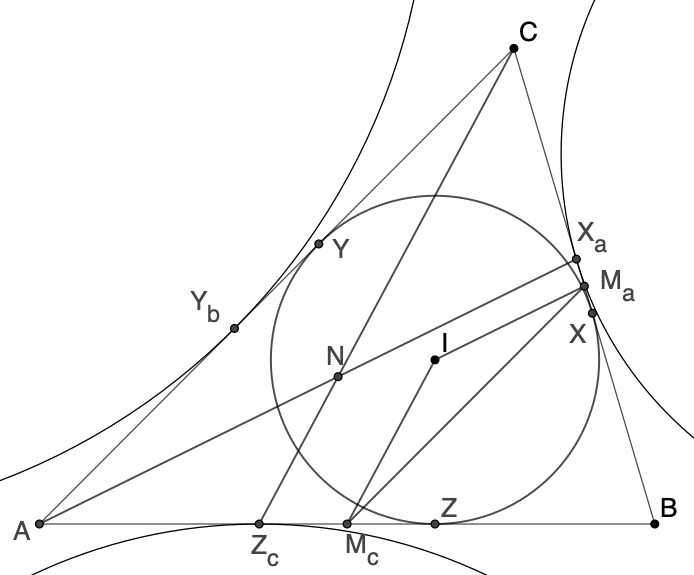
Der Abschnitt von einem Eckpunkt bis zum Nagelpunkt ist doppelt so lang wie die Strecke vom Inkreismittelpunkt zur entsprechenden Seitenmitte.
Für den Beweis wird das Beispiel |CN| = 2·|IMc| genommen. Vergleicht man die beiden Dreiecke △McIMa und △ANC, so ist IMc||CN und IMa||AN.
Zusätzlich gilt AC||MaMc nach dem Satz, dass die Verbindung von Seitenmittelpunkten parallel zur entsprechenden Dreiecksseite ist.
Also sind die Dreiecke △McIMa und △ANC ähnlich.
Weiterhin gilt, dass |AC| = 2·|MaMc|. Also gilt das auch für die anderen, entsprechenden Seiten in den beiden ähnlichen Dreiecken, also |CN| = 2·|IMc| und auch |AN| = 2·|IMa|.

Nun zum eigentlichen Satz
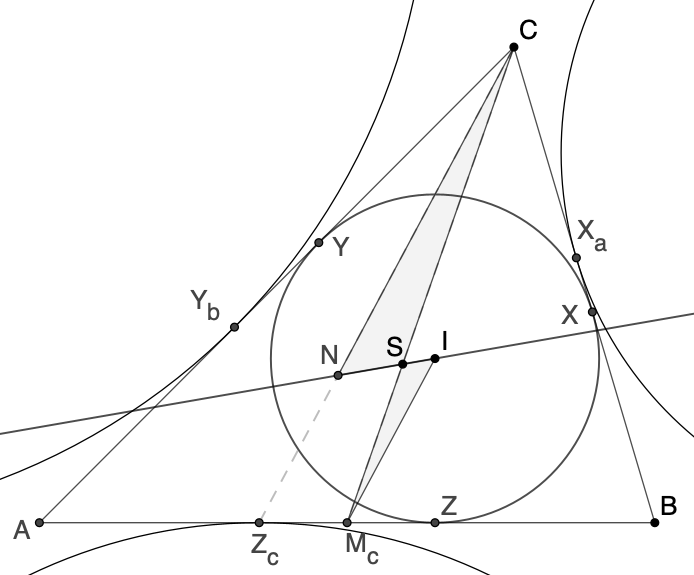Die Geraden NI und CMc schneiden sich in einem Punkt S. Von diesem soll nun nachgewiesen werden, dass es der Schwerpunkt des Dreiecks △ABC ist.
Da, wie bereits bewiesen, IMc||CN ist, sind die Dreiecke △NSC und △S McI ähnlich.
Für die beiden entsprechenden Seiten NC und IMc gilt laut dem bewiesenen Hilfsatz: |NC| = 2·|IMc|.
Also gilt das auch für die anderen, entspechenden Seiten. Damit gilt |CS| = 2·|SMc|. Das ist gerade das charakteristische Teilungsverhältnis für den Schwerpunkt auf einer Seitenhalbierenden. Damit ist S der Schwerpunkt des Dreiecks △ABC.
Und zusätzlich ist bewiesen, dass |NS| = 2·|SI|.

R. Albers, erstellt mit GeoGebra