Behauptung


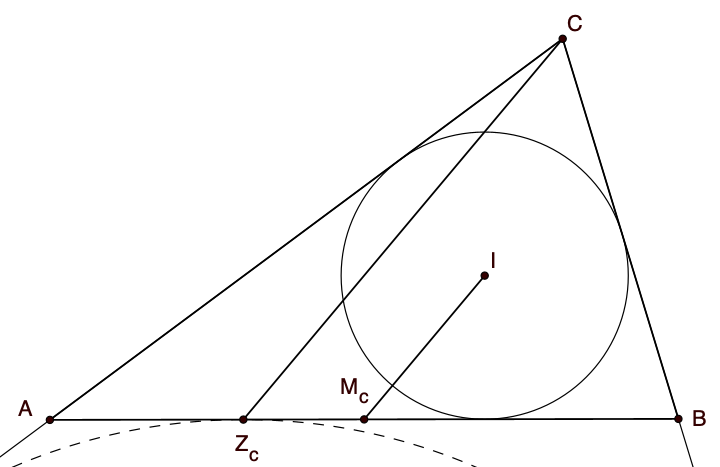
Die allgemeine Aussage wird hier für folgendes exemplarisches Beispiel formuliert:
Die Gerade durch den Seitenmittelpunkt Mc und den Inkreismittelpunkt I ist parallel zur Geraden durch den Ankreisberührpunkt Zc und der Ecke C.
Formal: McI || ZcC

Beweis
 Christian Heinrich von Nagel (1803 - 1882) hat in seinen Beweisen die Methode bevorzugt, Strecken zu Flächen zu erweitern und diese zu addieren, zu subtrahieren oder zu vergleichen. Der folgende Beweis ist der Originale von Nagel (§94) in aktueller Notation.



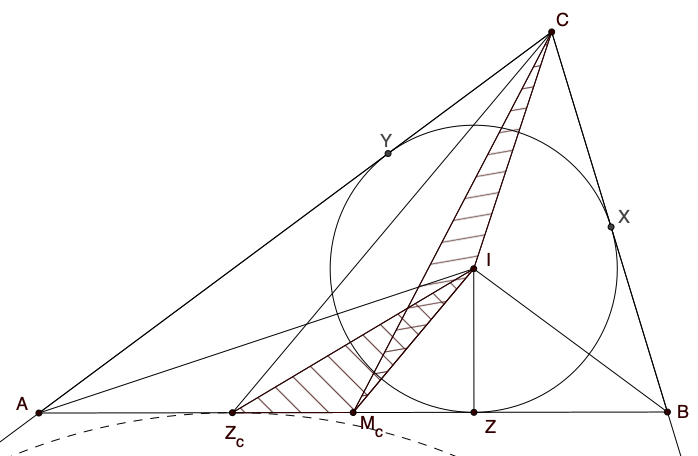
Beweisidee
Es wird gezeigt, dass die Dreiecke ZcMcI und McIC einen gleichgroßen Flächeninhalt haben. Wegen der gemeinsamen Grundseite McI müssen dann deren Höhen gleich lang sein. Also ist der Abstand von ZcC zu McI überall der gleiche, also sind beide Geraden parallel.

a) Bestimmung von Dreieck ZcMcI
Ankreisberührpunkt Zc und Inkreisberührpunkt Z sind von den Eckpunkten A bzw. B gleich weit entfernt (siehe hier). |AZc| = |ZB|. Damit gilt auch |ZcMc| = |McZ|.
Also gilt für den Flächeninhalt |△ZcMcI| = |△McZI| = 12\frac{1}{2}|△ZcZI|.
Da die Tangentenabschnitte von einem Punkt an einen Kreis gleich lang sind, gilt:
|ZcZ| = |AZ| - |AZc| =  |AZ| - |ZB| = |AY| - |XB| = |AY| + |YC| - |CX| - |XB| = |AC| - |CB|.
Diese Gleichung (die äußersten Ausdrücke), mit dem Inkreisradius als Höhe multipliziert, ergibt als Dreiecksflächen |△ZcZI| = |△AIC| - |△BCI|. Für die erste, angestrebte Fläche ergibt sich dann
|△ZcMcI| = 12\frac{1}{2} (|△AIC| - |△BCI|)

b) Bestimmung von Dreieck McIC
Es ist |△McIC| + |△AMcC| = |△AMcI| + |△AIC|, also |△AMcC| = |△AMcI| + |△AIC| - |△McIC|
|△McBC| = |△McIC| + |△McBI| + |△BCI|
Da |△AMcC| = |△McBC|, kann man beide rechten Seiten gleichsetzen.
|△AMcI| + |△AIC| - |△McIC| = |△McIC| + |△McBI| + |△BCI|
Aufgelöst nach dem gesuchten Dreieck McIC ergibt sich
2·|△McIC| = |△AMcI| + |△AIC| - |△McBI| - |△BCI|
Alle Dreiecke auf der rechten Seite haben den Inkreisradius als Höhe. Wegen |AMc| = |McB| heben sich der erste und dritte Flächeninhalt auf. Es bleibt
|△McIC| = 12\frac{1}{2} (|△AIC| - |△BCI|)
Damit sind also die beiden fraglichen Dreiecke ZcMcI und McIC gleich groß. Wegen ihrer gemeinsamen Seite McI sind ihre diesbezüglichen Höhen gleich lang. Also sind die Geraden McI und ZcC parallel.

Zurück

R. Albers, erstellt mit GeoGebra