Abschnitte auf den Dreiecksseiten

Der Inkreis und die drei Ankreise teilen durch ihre Berührpunkte die Dreiecksseiten bzw. deren Verlängerung in markante Abschnitte. Diese sind in der nachfolgenden Zeichnung farbig hervorgehoben.

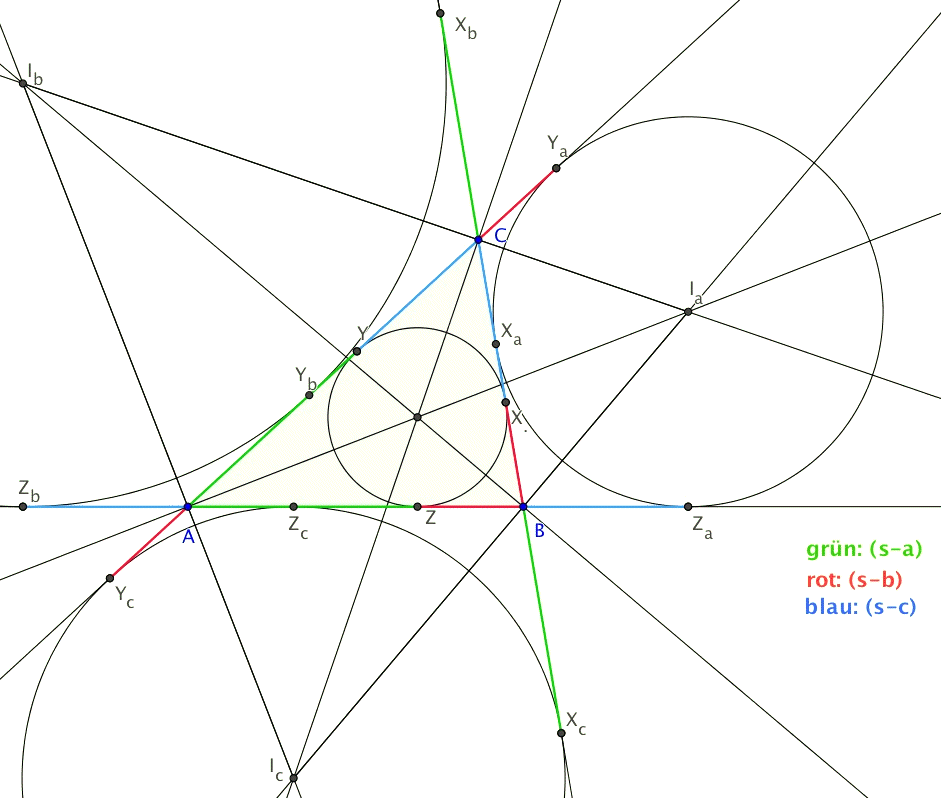
Herleitung

Die Herleitung für die Abschnitte, die die Berührpunkte des Inkreises auf den Dreiecksseiten bilden, findet man hier.

Die Strecken AZ_a und AY_a sind aus Symmetriegründen gleich lang. Mit (bekannten) Abschnitten und noch zu findenden Abschnitten ergibt sich:
|AY_a| = (s-a) + (s-c) + |CY_a| und |AZ_a| = (s-a) + (s-b) + |BZ_a|

Wegen |AZ_a| = |AY_a| folgt (s-c) + |CY_a| = (s-b) + |BZ_a| (1)

Wegen |BZ_a| = |BX_a| und |CY_a| = |CX_a| gilt: |BC| = (s-b) + (s-c) = |BZ_a| + |CY_a| (2)

(1) - (2) ergibt: |CY_a| - (s-b) = (s-b) - |CY_a| , woraus sofort |CY_a| = (s-b) folgt.

Eingesetzt in (1) ergibt sich |BZ_a| = (s-c)

Auf analoge Weise kann man die übrigen Streckenlängen von einem Eckpunkt bis zum nächsten Ankreisberührpunkt bestimmen (siehe farbige Markierung in der obigen Zeichnung).

Das bedeutet: An einer Dreiecksseite liegen der Berührpunkt des Inkreises und der Berührpunkt des zugehörigen Ankreises symmetrisch zum Mittelpunkt der Strecke.
Das bedeutet z.B. für die oben betrachtete Strecke BC: |CX| = |BX_a| = (s - c)

Weiterhin ergibt sich: |AZ_a| = |BX_b| = |CY_c| = (s-a) + (s-b) + (s-c) = 3s - (a+b+c) = s
D.h. von einem Eckpunkt bis zum "gegenüber liegenden" Ankreisberührpunkt ist die Entfernung immer s, also der halbe Dreiecksumfang.

R. Albers, Erstellt mit GeoGebra