Behauptung
Die drei Ecktransversalen für den Nagelpunkt schneiden sich in einem Punkt.



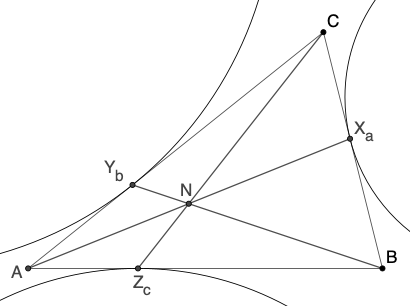
Beweis
Der Beweis ist eine Standardanwendung für die Umkehrung des Satzes von Ceva.
Dafür muss man zeigen, dass der Ausdruck |AZc||ZcB|·|BXa||XaC|·|CYb||YbA|\frac{|AZ_c|}{|Z_cB|}·\frac{|BX_a|}{|X_aC|}·\frac{|CY_b|}{|Y_bA|} den Wert 1 hat.
Entsprechend der Herleitung hier gilt: |AZc| = (s - b) , |ZcB| = (s - a) , u.s.w.
Damit wird der Bruch-Ausdruck zu  s−bs−a·s−cs−b·s−as−c\frac{s-b}{s-a}·\frac{s-c}{s-b}·\frac{s-a}{s-c} = 1, da sich alles wegkürzt. Dann hat aber auch der erste Bruch-Ausdruck den Wert 1, was gezeigt werden sollte.
Zurück

R. Albers Erstellt mit GeoGebra