Rationale Krylovraummethoden zur Modellreduktion von LZI Systemen
| Arbeitsgruppe: | Ehemalige AG Numerik |
| Leitung: | Prof. Dr. Angelika Bunse-Gerstner (E-Mail: bunse-gerstner@math.uni-bremen.de ) |
| Bearbeitung: | Dr. Dorota Kubalinska |
| Projektförderung: | „Scientific Computing in Engineering“ Doctorate Programme (University of Bremen) |
| Projektpartner: | ITEM, Universität Bremen |
| Laufzeit: | 01.10.2004 - 30.09.2007 |
 Eine wesentliche Aufgabe der Modellreduktion besteht darin, für ein großdimensionales lineares zeitinvariantes dynamisches System (LZI-System):
Eine wesentliche Aufgabe der Modellreduktion besteht darin, für ein großdimensionales lineares zeitinvariantes dynamisches System (LZI-System):
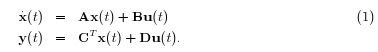
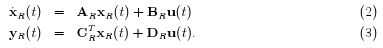
der Dimension n zu finden, das das dynamische Verhalten des Ausgangssystems annähernd wiedergibt. Dies wird bisher durch Approximation oder Hermite-Interpolation (Momentenanpassung) der Transferfunktion H(s) = CT (sI - A)-1 B des Ausgangssystems zu erreichen versucht. Für sehr große Dimensionen, wie etwa in der Datenassimilation des oben beschriebenen Teilprojekts, kann man im Wesentlichen nur versuchen, den Interpolationsansatz zu verfolgen. Dazu berechnet man Basen geeigneter rationaler Krylovräume zu den gewählten Interpolationspunkten. Das reduzierte System erhält man hiermit durch Projektion des Ausgangssystems.
Bei der Konstruktion von solchen ordnungsreduzierten Systemen ist es oft von entscheidender Bedeutung, wesentliche nach außn wirkende Eigenschaften der Ausgangssysteme zu erhalten, insbesondere wenn es sich um Subsysteme in einem komplexen System handelt, bei dem diese Eigenschaften das Gesamtsystemverhalten bestimmen.
Die Hauptzielrichtung derzeitiger Forschung ist es, die zwei Arten von Approximationsmethoden, nämlich Balancierung und Momentenanpassung, zu kombinieren. Dabei strebt man an, iterative Methoden zu entwickeln, die einerseits näherungsweise balancierte Reduktion erzielen und andererseits für Systeme sehr großer Dimensionen sowie für Implementierung auf parallelen Rechnern geeignet sind.
In diesem Projekt werden zwei Probleme bearbeitet:
- Es wird mit Hilfe von Ergebnissen uber rationale Interpolation und Approximation sowie Experimenten untersucht, welche Wahl der Interpolationspunkte (Entwicklungspunkte der Momente) eine möglichst gute Näherung an das Verhalten des Ausgangssystems ermöglicht [?]. Ein neuer Ansatz wird verfolgt, bei dem zwar rationale Krylovräume zur Berechnung der Projektion herangezogen werden, aber im Fall von mehrfach Ein- bzw. Ausgängen keine echte Interpolation der Transferfunktion, sondern eine Interpolation der Transferfunktion nur für gewisse Richtungen erzielt wird.
- Für passive Systeme werden basierend auf [?, ?, ?], und für System zweiter und höherer Ordnung basierend auf [?, ?, ?, ?], rationale Krylovraum-Methoden entwickelt und untersucht, die jeweils diese Eigenschaft für das reduzierte System erhalten können.

