A fundamental objective of model reduction consists in finding a system with much smaller dimensions for a linear time-invariant dynamic system (LTI system) with large dimensions, where the latter is with dimension N and m inputs, p outputs and constant matrices of coefficients, and the former with dimension n, whereby said system with smaller dimensions approximately reproduces the dynamic behaviour of the initial system [?]. Previous attempts to achieve this have involved approximation or Hermite interpolation (matching of moments) of the transfer function H(s) = C^T (_sI - A)^-1 B of the initial system. For very large dimensions, as in the data assimilation of the above-described sub-project, one can basically only try to follow the interpolation approach [?]. This is done by computing bases of suitable rational Krylov spaces for the selected interpolation points. The reduced system is thus obtained by projection of the initial system. When constructing order-reduced systems of this type it is often of critical importance to retain essential externally acting properties of the initial systems, particularly where one is dealing with subsystems in a complex system, where these properties determine the behaviour of the complete system.

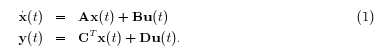
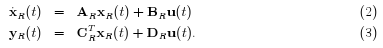
The main objective of the current research is to combine two types of approximation procedure, namely balancing and matching of moments. We are striving to develop iterative methods which, on the one hand, achieve approximately balanced reduction and, on the other, are suitable for systems of very large dimensions as well as implementation on parallel computers.

This project is addressing two problems:

• With the aid of results using rational interpolation and approximation, as well as experiments, we are investigating which choice of interpolation points (development points of the moments) makes it possible to achieve the best possible approximation to the behaviour of the initial system [?]. We are following a new approach in which rational Krylov spaces are being drawn on to compute the projection, but in the case of multiple inputs or outputs no real interpolation of the transfer function is achieved, but rather an interpolation of the transfer function for specific directions only.
• For passive systems, the work contained in [?, ?, ?] is being used as the basis for the development and investigation of rational Krylov space methods which can each conserve this property for the reduced system, and the work contained in [?, ?, ?, ?] as the basis for systems of second and higher order.