Konstruktion von Coorbit-Räumen und Wavelet-Banach-Frames auf homogenen Räumen
| Leitung: | |
| Bearbeitung: | Prof. Dr. Gerd Teschke |
| Projektförderung: | EU (HASSIP-Netzwerk) |
| Projektpartner: |
Prof. Dr. Stephan Dahlke, Philipps-Universität Marburg; AG Numerik / Wavelet-Analysis Prof. Dr. Gabriele Steidl, Universität Mannheim |
| Laufzeit: | seit 01.08.2001 |
 Das Konzept der Darstellung von Funktionen mithilfe von Frames wurde in den fünfziger Jahren für Hilbert-Raum-Strukturen entdeckt. Ausgehend von quadratintegrierbaren Gruppendarstellungen in Hilbert-Räumen wurde diese Theorie in den achtziger Jahren auch für allgemeinere Banach-Räume weiterentwickelt. Ausgangspunkt war die Einführung so genannter Coorbit-Räume. Diese Räume ermöglichen u.a. die Charakterisierung von Modulations-Räumen (Glattheitsräume für die Gabor-Analysis) oder Besov-Räumen (Glattheitsräume der Wavelet-Analysis). Will man nun Frames in diesen Räumen konstruieren, besteht die Kernidee in der Diskretisierung der Gruppendarstellung (in einem entsprechenden Hilbert-Raum) nach bestimmten, technischen Kriterien, d.h. man wählt ein geeignetes Gitter auf der Gruppe und erzeugt somit über die Darstellung der Gruppe die analysierenden Atome, die dann in ihrer Gesamtheit als Frame bezeichnet werden.
Ein Beispiel für eine Mannigfaltigkeit ist die Sphäre (hier S1, linkes Bild).
Dazu betrachten wir den L2(S1) und die Euklidische Gruppe E,
die über ihre Darstellung in L2(S1) die Gabor-Transformation auf S1 induziert.
Anstatt E muss hier ein Quotient E/H gewählt werden,
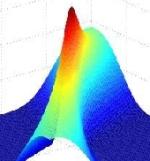
um Quadratintegrierbarkeit zu gewährleisten. Ein zulässiges Wavelet-Atom ist im rechten Bild zu sehen.
Das Konzept der Darstellung von Funktionen mithilfe von Frames wurde in den fünfziger Jahren für Hilbert-Raum-Strukturen entdeckt. Ausgehend von quadratintegrierbaren Gruppendarstellungen in Hilbert-Räumen wurde diese Theorie in den achtziger Jahren auch für allgemeinere Banach-Räume weiterentwickelt. Ausgangspunkt war die Einführung so genannter Coorbit-Räume. Diese Räume ermöglichen u.a. die Charakterisierung von Modulations-Räumen (Glattheitsräume für die Gabor-Analysis) oder Besov-Räumen (Glattheitsräume der Wavelet-Analysis). Will man nun Frames in diesen Räumen konstruieren, besteht die Kernidee in der Diskretisierung der Gruppendarstellung (in einem entsprechenden Hilbert-Raum) nach bestimmten, technischen Kriterien, d.h. man wählt ein geeignetes Gitter auf der Gruppe und erzeugt somit über die Darstellung der Gruppe die analysierenden Atome, die dann in ihrer Gesamtheit als Frame bezeichnet werden.
Ein Beispiel für eine Mannigfaltigkeit ist die Sphäre (hier S1, linkes Bild).
Dazu betrachten wir den L2(S1) und die Euklidische Gruppe E,
die über ihre Darstellung in L2(S1) die Gabor-Transformation auf S1 induziert.
Anstatt E muss hier ein Quotient E/H gewählt werden,
um Quadratintegrierbarkeit zu gewährleisten. Ein zulässiges Wavelet-Atom ist im rechten Bild zu sehen.
Viele mathematische Sachverhalte erfordern nun aber eine spezielle Wahl des zugrunde liegenden Hilbert-Raumes, z.B. den L2(S1). In diesen Fällen ist die Gruppendarstellung häufig nicht mehr quadratintegrierbar, weshalb die Frame-Konstruktion über die Coorbit-Theorie nicht mehr so ohne weiteres funktioniert. Der Ausweg besteht nun darin, nicht die volle sondern nur einen Teil der Gruppe – einen so genannten Quotienten oder homogenen Raum – zu betrachten. Dadurch erhält man zwar nur abgeschwächte Formen von Quadratintegrierbarkeit, aber die Prinzipien der Frame-Konstruktion können übertragen werden. Somit kann man wieder Glattheitsräume einführen, Frames in diesen konstruieren und Approximationsresultate beweisen. Ein weiteres Potential der entwickelten Coorbit- Theorie besteht in der Konstruktion gemischter Glattheitsräume. Beispielsweise kann man ausgehend von der gemischten affinen Weyl-Heisenberg-Gruppe "interpolierende" Räume (d.h. Funktionenräume zwischen Modulations- und Besov-Räumen) und entsprechende Frames in ihnen konstruieren. Die Konstruktion von Frames basiert auf einer Diskretisierung der Gruppe (oder des Quotienten E/H). Die entsprechenden Frame-Operatoren hängen vom Reproduktionskern ab, der an diesen diskreten Gruppen-Gitterpunkten ausgewertet werden muss (linkes Bild). Dieser Kern muss außerdem bestimmte Oszillationsbeschränkungen erfüllen. Der entsprechende Oszillationskern ist im rechten Bild dargestellt.



