Geschaltete Systeme, konvexe Kegel und Lyapunov-Funktionen
| Leitung: | Prof. Dr. Fabian Wirth |
| Bearbeitung: | |
| Projektförderung: | Science Foundation Ireland |
| Projektpartner: |
Prof. Dr. A. Berman, Technion, Israel Dr. Robert Shorten, Hamilton Institute, NUI Maynooth, Irland Prof. Dr. T. Laffey, University College Dublin, Irland Prof. Dr. K. S. Narendra, Yale University, USA |
| Laufzeit: | seit 01.04.2004 |
 Dynamische Systeme werden als geschaltete Systeme bezeichnet, wenn sie aus der Kopplung eines Systems mit kontinuierlichem Zustand (in diskreter oder kontinuierlicher Zeit) mit einem logik-basierten System, etwa einem endlichen Automaten, bestehen. Systeme von diesem Typ treten in vielen Anwendungszusammenhängen auf, z.B. bei der Kontrolle von Internetdatentransfer oder der Beschreibung der Dynamik von ABS-Bremssystemen. Wesentliche Fragen hinsichtlich der Analyse der Dynamik und des Entwurfs derartiger Systeme sind ungeklärt, trotz aller Fortschritte der letzten Jahre. Insbesondere fehlen systematische Entwurfsverfahren. Das Ziel dieses Projektes ist es, Unterstützung für die Synthese stabiler geschalteter Systeme zu liefern, indem einfach verifizierbare Bedingungen für die Existenz von gemeinsamen Lyapunov-Funktionen allgemeinen Typs entwickelt werden. Aufbauend auf Arbeiten zur Existenz gemeinsamer quadratischer Lyapunov- Funktionen sollen dabei neue Kriterien durch die Analyse breiterer Klassen von Lyapunov- Funktionen entwickelt werden. Dabei ist eine Reihe von Fragen zu untersuchen, die den Schnitt konvexer Mengen von Matrizen betreffen.
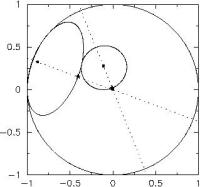
Parametrisierte Darstellung der Kegel von Lyapunov-Funktionen für zwei Matrizen
Dynamische Systeme werden als geschaltete Systeme bezeichnet, wenn sie aus der Kopplung eines Systems mit kontinuierlichem Zustand (in diskreter oder kontinuierlicher Zeit) mit einem logik-basierten System, etwa einem endlichen Automaten, bestehen. Systeme von diesem Typ treten in vielen Anwendungszusammenhängen auf, z.B. bei der Kontrolle von Internetdatentransfer oder der Beschreibung der Dynamik von ABS-Bremssystemen. Wesentliche Fragen hinsichtlich der Analyse der Dynamik und des Entwurfs derartiger Systeme sind ungeklärt, trotz aller Fortschritte der letzten Jahre. Insbesondere fehlen systematische Entwurfsverfahren. Das Ziel dieses Projektes ist es, Unterstützung für die Synthese stabiler geschalteter Systeme zu liefern, indem einfach verifizierbare Bedingungen für die Existenz von gemeinsamen Lyapunov-Funktionen allgemeinen Typs entwickelt werden. Aufbauend auf Arbeiten zur Existenz gemeinsamer quadratischer Lyapunov- Funktionen sollen dabei neue Kriterien durch die Analyse breiterer Klassen von Lyapunov- Funktionen entwickelt werden. Dabei ist eine Reihe von Fragen zu untersuchen, die den Schnitt konvexer Mengen von Matrizen betreffen.
Parametrisierte Darstellung der Kegel von Lyapunov-Funktionen für zwei MatrizenEs ist bekannt, dass die Frage nach gemeinsamen quadratischen Lyapunov-Funktionen für eine Menge von Hurwitz-stabilen Matrizen eng mit der Struktur des Schnitts der Kegel der Lyapunov-Funktionen für die einzelnen Matrizen zusammenhängt. Im Allgemeinen ist die Struktur dieser Schnittmenge nur schlecht verstanden, aber in wichtigen Spezialfällen können elegante und effiziente Kriterien angegeben werden, mit deren Hilfe die Frage nach der Existenz einer gemeinsamen Lyapunov-Funktion beantwortet werden kann. Im theoretischen Teil dieses Projekts geht es um die Untersuchung von konvexen Matrizenkegeln, die auf natürliche Weise bei der Untersuchung von Lyapunov-Funktionen von ganz allgemeinem Typ auftreten. Besondere Beachtung wird dabei der Stabilität positiver linearer Systeme zukommen, für die es ausreicht, copositive Lyapunov-Funktionen zu untersuchen. Ein besonderer Schwerpunkt des Projekts wird auf geschalteten Systemen mit einfachem Eingang und Ausgang liegen, sowie auf geschalteten positiven Systemen und auf einer Klasse von geschalteten Systemen, die bei der Untersuchung der Dynamik von Internetdatentransfer eine wichtige Rolle spielt.