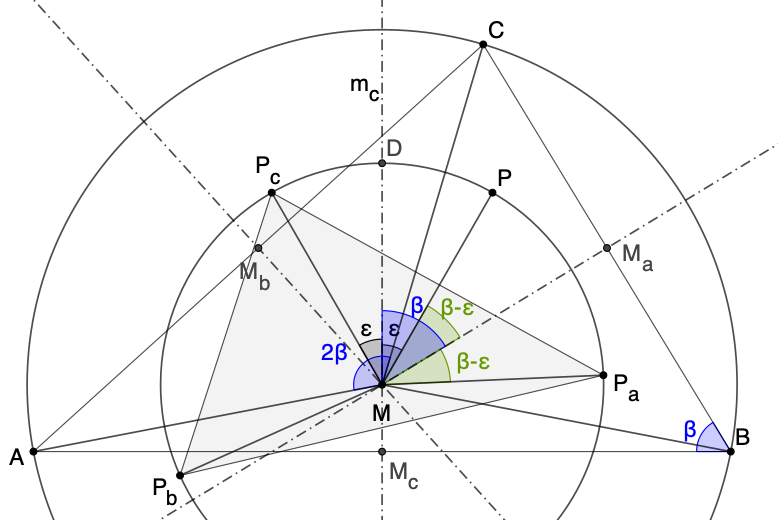
Das Spiegeln eines Punktes P an den drei Mittelsenkrechten m_a, m_b, m_c eines Dreiecks ABC ergibt die Punkte P_a, P_b, P_c. Dann ist das Dreieck P_aP_bP_c ähnlich zum Dreieck ABC.

Beweis
Es sei M der Schnittpunkt der drei Mittelsenkrechten, also der Umkreismittelpunkt des Dreiecks ABC. Dann sind die Strecken MP_a, MP_b und MP_c gleich lang, da sie Bilder der Strecke MP sind. Also ist M auch der Umkreismittelpunkt des Dreiecks P_aP_bP_c . Für die Ähnlichkeit der beiden Dreiecke muss nur noch gezeigt werden, dass die entsprechenden Winkel mit dem Scheitel M gleich groß sind. Das geschieht hier exemplarisch für die Winkel ∡CMA und ∡P_aMP_c.
Sei wie üblich |∡CBA| = β . Dann ist der zugehörige Mittelpunktswinkel |∡CMA| = 2β.
Sei der Winkel von PM zu m_c gleich ε. Dann ist der gespiegelte Winkel zwischen m_c und MP_c ebenfalls ε (grau). Der Winkel zwischen m_a und m_c ist β. Also ist |∡M_aMP| = β - ε (grün). Wegen der Spiegelung an m_a ist auch |∡P_aMM_a| = β - ε (grün). Dann ist |∡P_aMP_c.| = ε + β + β - ε = 2β. Damit sind ∡CMA und ∡P_aMP_c. gleich groß.

Für die anderen Punkte und andere Lagebeziehungen ergeben sich analoge Rechnungen.
Damit sind entsprechende Winkel in den Dreiecken P_aP_bP_c und ABC gleich groß und die Dreiecke sind ähnlich.

R. Albers, erstellt mit GeoGebra