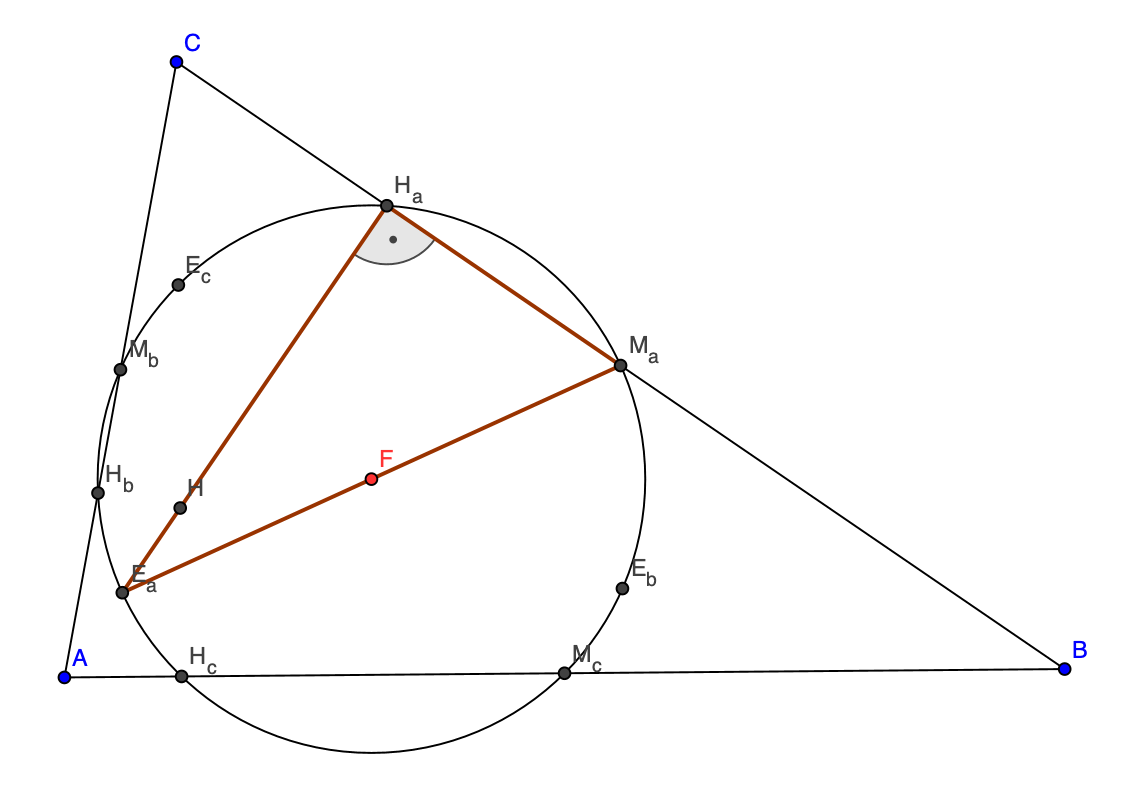
Beweis, 1.Teil
Ma, Mb, Mc und Ea, Eb, Ec liegen auf einem Kreis

 

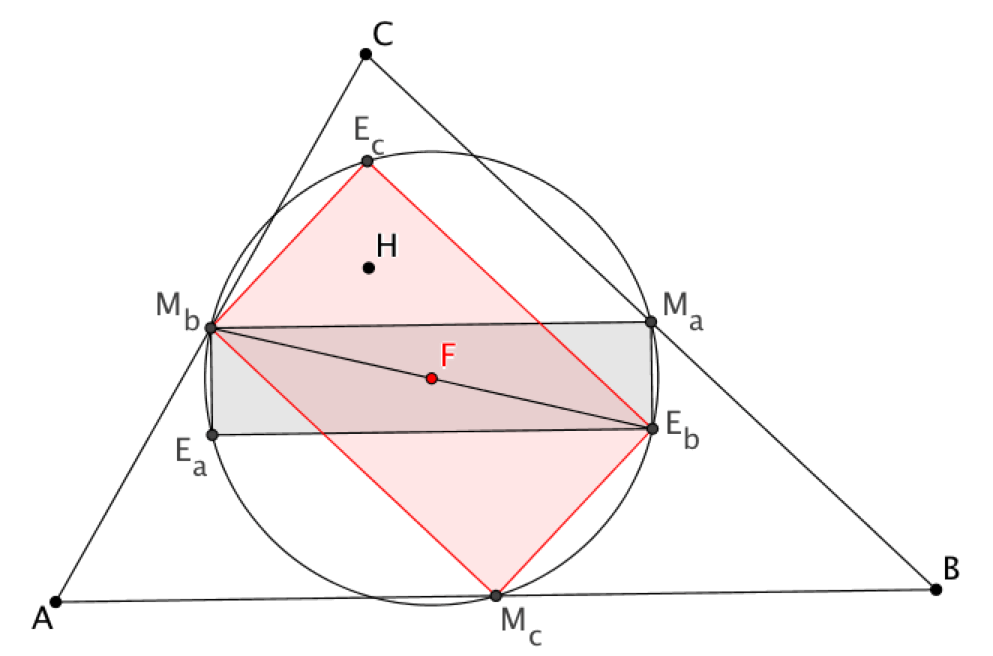
Beweisidee: Man zeigt, dass die Vierecke MaMbEaEb und MbMcEbEc Rechtecke sind. Dann besitzen sie Umkreise welche die Ecken enthalten. Da die beiden Vierecke eine gemeinsame Diagonale MbEb haben, müssen die beiden Umkreise identisch sein.

Viereck MaMbEaEb
Nach der Umkehrung des 1. Strahlensatzes mit Strahlenzentrum H gilt:


Weiter gilt (Umkehrung des 1. Strahlensatzes mit Zentrum C):
EaEb||MaMb.

Analog gilt (Umkehrung des 1. Strahlensatzes mit Zentrum A):

und Zentrum B

Aus EaMb || HC und EbMa || HC EaMb || EbMa.

Da die Strecke HC als Teil der Höhe senkrecht zu Strecke AB ist, sind die vier Innenwinkel rechte Winkel und das Viereck MaMbEaEb ist ein Rechteck.

Viereck EbEcMbMc
 Es gilt (Umkehrung des 1. Strahlensatzes mit Zentrum H):

Weiter gilt (Umkehrung des 1. Strahlensatzes mit Zentrum A):


Aus EcMb || HA und EbMc || HA folgt EcMb || EbMc.

Da die Strecke HA als Teil der Höhe senkrecht zu Strecke BC ist, ist das Viereck MbMcEbEc ein Rechteck.

Beide Rechtecke MaMbEaEb und MbMcEbEc haben jeweils einen Umkreis, bei dem die Strecken MaEa, MbEb und McEc jeweils Durchmesser sind. Wegen des gemeinsamen Durchmessers MbEb sind beide Umkreise identisch. Folglich liegen alle sechs Punkte auf einem Kreis, dem Feuerbach-Kreis.

Beweis, 2.Teil
Die Höhenfußpunkte Ha, Hb, Hc liegen ebenfalls auf dem Feuerbach-Kreis

 

Der Punkt Ea liegt auf der Höhe ha, welche senkrecht zur Dreiecksseite BC ist. Daraus folgt, dass der Winkel EaHaMa 90° groß ist. Nach der Umkehrung des Satz des Thales liegt Ha also auf dem Kreis mit dem Durchmesser EaMa. Da EaMa aber auch ein Durchmesser des Feuerbachkreises war, liegt Ha auf diesem.
In analoger Weise zeigt man, dass auch Hb und Hc auf dem Feurbachkreis liegen.

zurück

Matthias Pahl, R.Albers, Erstellt mit GeoGebra