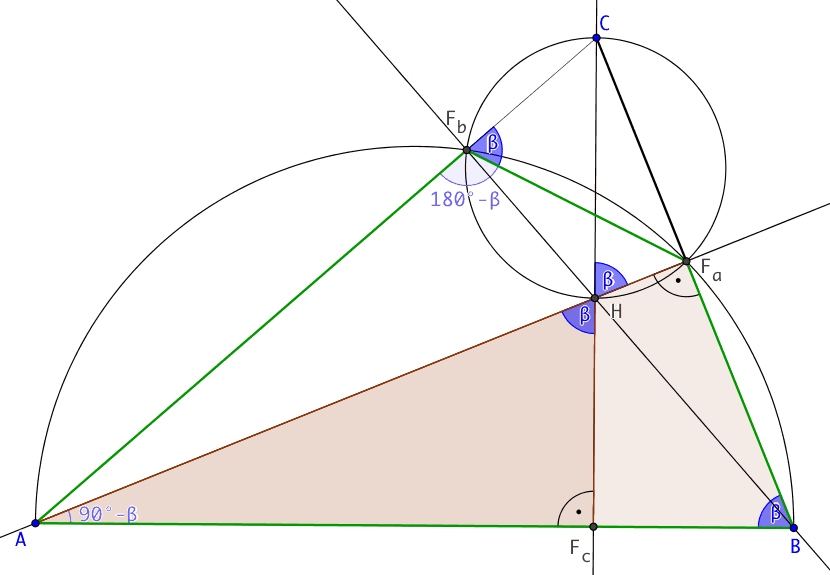
Wir gehen zunächst auf den spitzwinkligen Fall ein.
Es seien die Höhen von A (Fußpunkt Fa) und B (Fußpunkt Fb) gezeichnet. Der Schittpunkt beider Höhen ist H. Wir zeichnen nun die Strecke CH und fällen von H das Lot auf AB (Fußpunkt Fc). Es ist nun zu zeigen, dass C, H und Fc auf einer Geraden liegen. Dazu zeigen wir, dass |∠AHFc| = |∠FaHC|.

Wie üblich sei |∠CBA| = β.

Dann ist im rechtwinkligen Dreieck ABFa bei A |∠FaAB| =90°-β
und im rechtwinkligen Dreieck AFcH |∠AHFc| = β.

Der Thaleskreis über AB verläuft durch Fa und Fb. Damit ist das Viereck ABFaFb (oben in Grün) ein Sehnenviereck und der Winkel bei Fb |∠AFbFa| =180°-β. Der Nebenwinkel ∠FaFbC ist dann β.
Wegen der rechten Winkel bei Fa und Fb liegen diese Punkte auf dem Thaleskreis über der Strecke CH.
Die beiden Winkel ∠FaFbC und ∠FaHC sind Peripheriewinkel über der gemeinsamen Sehne FaC.
Folglich ist |∠FaHC| = β.

Damit gilt |∠AHFc| = |∠FaHC|. q.e.d.

Im rechtwinkligen Fall schneiden sich die drei Höhen im Scheitelpunkt des rechten Winkels.

Im stumpfwinkligen Fall kann man die gleiche Argumentation anwenden wie im spitzwinkligen Fall.

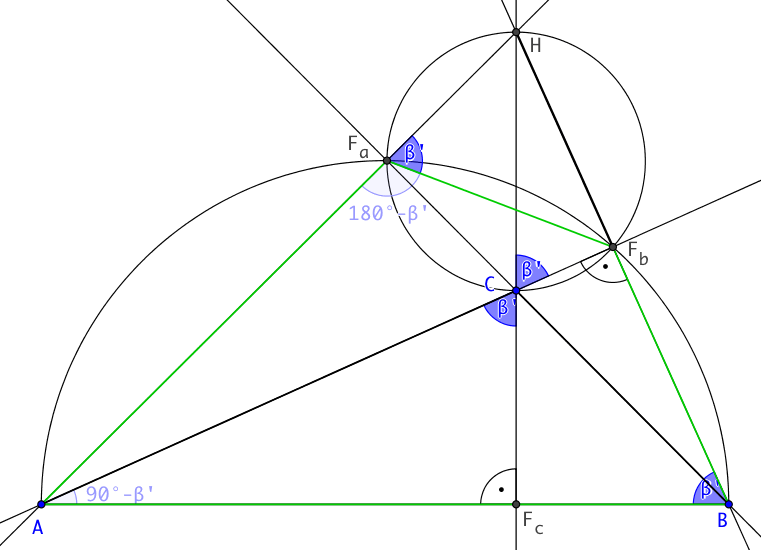
Hier wird allerdings mit dem Winkel |∠FbBA| = β' argumentiert.

Reimund Albers, erstellt mit GeoGebra