Bilevel Optimal Control
| Working Group: | WG Optimization and Optimal Control |
| Leadership: | Prof. Dr. Christof Büskens ((0421) 218-63861, E-Mail: bueskens@math.uni-bremen.de ) |
| Processor: | Dr. Matthias Knauer ((0421) 218-63863, E-Mail: knauer@math.uni-bremen.de) |
| Project partner: | |
| Time period: | 01.04.2004 - 30.04.2009 |
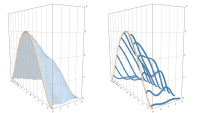
 Für eine optimale Lösung des übergeordneten Problems muss sichergestellt werden, dass das in der Beschränkung genannte untergeordnete Problem, das von der optimalen Lösung des übergeordneten Problems abhängig ist, lösbar ist.
Für eine optimale Lösung des übergeordneten Problems muss sichergestellt werden, dass das in der Beschränkung genannte untergeordnete Problem, das von der optimalen Lösung des übergeordneten Problems abhängig ist, lösbar ist.Genauso wie ein Optimalsteuerungsproblem einen dynamischen Prozess über die Zeit abbildet, kann auch die Kopplung zwischen den beiden Ebenen des Bilevel-Optimalsteuerungsproblems von der Zeit abhängig sein. Zur Lösung von klassischen Optimalsteuerungsproblemen wird das System entlang der Zeitachse diskretisiert, um numerische Verfahren anwenden zu können. Bei einem Bilevel-Optimalsteuerungsproblem mit zeitabhängiger Kopplung müssen zusätzlich noch diskrete Zeitpunkte ausgewählt werden, zu denen die untergeordneten Optimalsteuerungsprobleme berücksichtigt werden, die dann wiederum einzeln diskretisiert werden.
Dadurch wird diese Aufgabenstellung numerisch sehr komplex. Zu jeder Lösung des übergeordneten Problems müssen gleichzeitig die ausgewählten untergeordneten Probleme gelöst werden, die auf anderen Zeitachsen erklärt sind.
Motiviert wurde diese Fragestellung der Bilevel-Optimierung durch die optimale Steuerung eines Kransystems: Als übergeordnetes Problem soll der Kran schwingungsfrei an eine andere Position gefahren werden. Während der Fahrt soll aber als untergeordnetes Problem sichergestellt sein, dass der Kran jederzeit auf Anforderung auch innerhalb einer vorgegebenen Zeit angehalten werden kann.
Das Thema dieser Dissertation unter der Betreuung von Prof. Dr. Christof Büskens ist die Entwicklung einer geschlossenen Theorie und der Vergleich verschiedener Verfahren und Strategien zur Lösung von Optimalsteuerungsproblemen, insbesondere im Hinblick auf die
Optimale Steuerung eines Kransystems in Echtzeit.
Publications
- M. Knauer.
Bilevel-Optimalsteuerung mittels hybrider Lösungsmethoden am Beispiel eines deckengeführten Regalbediengerätes in einem Hochregallager.
Dissertationsschrift, Universität Bremen, 2009. - C. Büskens, M. Knauer.
Bilevel Optimization of Container Cranes.
5th MATHMOD Vienna International Conference on Mathematical Modelling, 08.02.-10.02.2006, Vienna, Austria.
ARGESIM Report Nr. , 30(2):SP18.3.1, 2006.